Sakrij rješenje
Kliknite ovdje kako biste prikazali rješenje.
Tvrdnju dokazujemo za proizvoljan 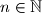 .
.
Svaku dužinu obojimo plavo ako je na njoj paran broj, a crveno ako je neparan. Primijetimo da imamo trokute samo s  ili
ili  crvene stranice.
crvene stranice.
Dokazat ćemo da točke možemo podijeliti u  skupa,
skupa, 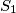 i
i 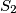 , tako da su sve dužine u svakom skupu plave. Uzmimo neku crvenu dužinu
, tako da su sve dužine u svakom skupu plave. Uzmimo neku crvenu dužinu  i pokušajmo konstruirati takva
i pokušajmo konstruirati takva  skupa.
skupa.
Ako ne postoji crvena dužina, možemo točke podijeliti u  skupa samo s plavim dužinama.
skupa samo s plavim dužinama.
U suprotnom, promatramo neku treću točku  . Očito
. Očito  i
i  moraju biti u različitim skupovima, pa stavimo
moraju biti u različitim skupovima, pa stavimo  u
u 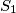 , a
, a  u
u 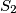 . Znamo da je točno jedna od dužina
. Znamo da je točno jedna od dužina 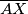 i
i 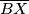 plava, pa
plava, pa  stavimo u
stavimo u 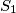 ako je
ako je 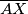 plava, a u
plava, a u 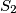 ako je
ako je 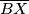 plava.
plava.
Po Dirichletovom principu, jedan od skupova 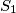 i
i 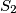 ima barem
ima barem 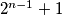 točaka koje su sve međusobno spojene plavim dužinama.
točaka koje su sve međusobno spojene plavim dužinama.
Sada u tom skupu brojeve na svim dužinama podijelimo s  i ponovimo opisani postupak podjele točaka na
i ponovimo opisani postupak podjele točaka na  skupa samo s plavim dužinama sve dok nam ne ostane skup od
skupa samo s plavim dužinama sve dok nam ne ostane skup od  točke. Te
točke. Te  točke povezane su dužinama na kojima su brojevi
točke povezane su dužinama na kojima su brojevi  ili
ili  , a zbog konstrukcije skupa, znamo da su sve dužine plave, odnosno na njima je broj
, a zbog konstrukcije skupa, znamo da su sve dužine plave, odnosno na njima je broj  . Time je zadatak završen.
. Time je zadatak završen.
 Školjka
Školjka 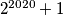 točaka. Na svakoj dužini koja spaja neke dvije točke nalazi se broj iz skupa
točaka. Na svakoj dužini koja spaja neke dvije točke nalazi se broj iz skupa 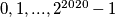 . Za svake
. Za svake  u ravnini vrijedi da je jedan od brojeva na dužinama
u ravnini vrijedi da je jedan od brojeva na dužinama 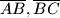 i
i  zbroj druga dva. Dokaži da postoji trokut u ravnini kojemu na svim stranicama pišu nule.
zbroj druga dva. Dokaži da postoji trokut u ravnini kojemu na svim stranicama pišu nule.