Točno
31. srpnja 2013. 18:58 (12 godine, 6 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Lako se indukcijom dokaže da je parno za parne
parno za parne  , odnosno neparno za neparne
, odnosno neparno za neparne  .
.
Nadalje, lako se pokaže sljedeća jednakost, za sve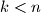 :
: 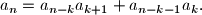 Motivacija za tu jednakost je raspisivanje rekurzije za elemente niza s desne strane jednakosti iz teksta zadatka,
Motivacija za tu jednakost je raspisivanje rekurzije za elemente niza s desne strane jednakosti iz teksta zadatka,  puta.
puta.
Iz te jednakosti, za parne (
(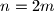 ) i za
) i za 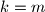 vrijedi
vrijedi 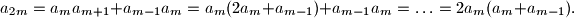
Sada se dalje opet dokazuje indukcijom: ako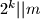 , tada (po pretpostavci indukcije)
, tada (po pretpostavci indukcije) 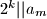 , pa onda iz zadnje jednakosti zaključujemo
, pa onda iz zadnje jednakosti zaključujemo 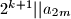 , jer je
, jer je 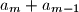 neparan broj.
neparan broj.
 parno za parne
parno za parne  , odnosno neparno za neparne
, odnosno neparno za neparne  .
.Nadalje, lako se pokaže sljedeća jednakost, za sve
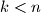 :
: 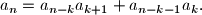 Motivacija za tu jednakost je raspisivanje rekurzije za elemente niza s desne strane jednakosti iz teksta zadatka,
Motivacija za tu jednakost je raspisivanje rekurzije za elemente niza s desne strane jednakosti iz teksta zadatka,  puta.
puta.Iz te jednakosti, za parne
 (
(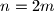 ) i za
) i za 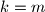 vrijedi
vrijedi 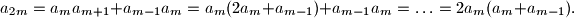
Sada se dalje opet dokazuje indukcijom: ako
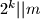 , tada (po pretpostavci indukcije)
, tada (po pretpostavci indukcije) 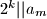 , pa onda iz zadnje jednakosti zaključujemo
, pa onda iz zadnje jednakosti zaključujemo 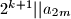 , jer je
, jer je 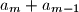 neparan broj.
neparan broj.  Školjka
Školjka  je zadan na ovaj način:
je zadan na ovaj način: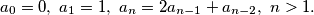
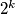 dijeli
dijeli