Neocijenjeno
31. listopada 2021. 14:25 (4 godine, 4 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
postavimo  u kompleksnu ravninu tako da je
u kompleksnu ravninu tako da je 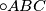 jedinična kružnica, te neka je točki
jedinična kružnica, te neka je točki  pridružen 1. U nastavku
pridružen 1. U nastavku  označava broj pridružen točki
označava broj pridružen točki  .
.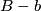 različit od 1
različit od 1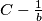 (jer je
(jer je 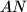 realna os)
realna os)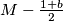
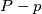
Kako je 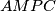 tetivan, imamo da je
tetivan, imamo da je 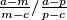 realan. Konjugiranjem sijedi:
realan. Konjugiranjem sijedi: 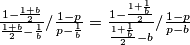 Zbog pretpostavke da je
Zbog pretpostavke da je  različita od
različita od  možemo kratiti
možemo kratiti 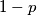 . Nakon sređivanja dobiva se jednadžba
. Nakon sređivanja dobiva se jednadžba 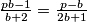 čije je rješenje
čije je rješenje 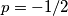 . Sada je trivijalno vidjeti
. Sada je trivijalno vidjeti 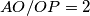 , pa zbog činjenice da je
, pa zbog činjenice da je 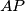 srednjica trokuta
srednjica trokuta 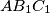 ,
,  je centar opisane kružnice i težište tog trokuta što daje da je
je centar opisane kružnice i težište tog trokuta što daje da je 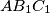 jednakostraničan
jednakostraničan
 Školjka
Školjka  takav da je
takav da je 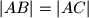 . Neka su
. Neka su  i
i  polovišta stranica
polovišta stranica  i
i  redom. Neka je
redom. Neka je 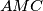 , različito od
, različito od  siječe opisanu kružnicu trokuta
siječe opisanu kružnicu trokuta  i
i  . Dokaži da je trokut
. Dokaži da je trokut