Točno
2. travnja 2022. 20:50 (3 godine, 10 mjeseci)
U trokutu

vrijedi
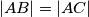
. Na stranici

nalazi se točka

takva da je
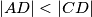
, a na dužini

točka

takva da je
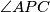
pravi kut. Ako je
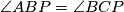
, odredi
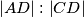
.
%V0
U trokutu $ABC$ vrijedi $\left\vert AB \right\vert = \left\vert AC \right\vert$. Na stranici $\overline{AC}$ nalazi se točka $D$ takva da je $\left\vert AD \right\vert < \left\vert CD \right\vert$, a na dužini $\overline{BD}$ točka $P$ takva da je $\angle{APC}$ pravi kut. Ako je $\angle{ABP} = \angle{BCP}$, odredi $\left\vert AD \right\vert : \left\vert CD \right\vert$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Prvo, iz $AB=AC$ i $\angle ABP= \angle BCP$ imamo:
$$\angle PCD=\angle DCB-\angle BCP=\angle ABC-\angle ABP=\angle DBC$$, pa su trokuti $DPC$ i $DCB$ slični. To daje $DC^2=DP*DB$. Promotrimo inverziju s centrom $D$ i radijusom $DC$. Zbog gornje relacije znamo da se $P$ i $B$ šalju jedna u drugu. Neka je $X$ točka u koju se šalje $A$. Vrijedi:
$90=\angle APD+\angle DPC=\angle DXB+\angle BCD$
Ovo jedinstveno određuje točku $X$ kao presjek $AC$ i okomice iz $B$ na $BC$, uočimo i $AX=AB$. Neka je sad $AD=x, DC=rx, AC=(r+1)x$. Iz definicije inverzije je:\\
$x*(r+2)x=r^2*x^2$, odakle $r=2$ i $AD:CD=1:2$
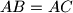 i
i 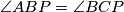 imamo:
imamo: 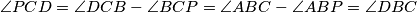 , pa su trokuti
, pa su trokuti 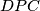 i
i 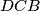 slični. To daje
slični. To daje 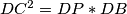 . Promotrimo inverziju s centrom
. Promotrimo inverziju s centrom  i radijusom
i radijusom 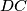 . Zbog gornje relacije znamo da se
. Zbog gornje relacije znamo da se  i
i  šalju jedna u drugu. Neka je
šalju jedna u drugu. Neka je  točka u koju se šalje
točka u koju se šalje  . Vrijedi:
. Vrijedi: 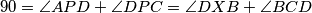 Ovo jedinstveno određuje točku
Ovo jedinstveno određuje točku  kao presjek
kao presjek  i okomice iz
i okomice iz  na
na  , uočimo i
, uočimo i 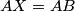 . Neka je sad
. Neka je sad 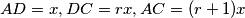 . Iz definicije inverzije je:
. Iz definicije inverzije je: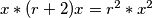 , odakle
, odakle 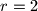 i
i 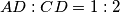
 Školjka
Školjka  vrijedi
vrijedi 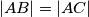 . Na stranici
. Na stranici  nalazi se točka
nalazi se točka 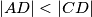 , a na dužini
, a na dužini  točka
točka 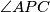 pravi kut. Ako je
pravi kut. Ako je 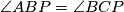 , odredi
, odredi 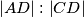 .
.