Neocijenjeno
25. rujna 2022. 11:34 (3 godine, 5 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
-ako kvadrate prebacimo na desnu stranu i redom na obje strane prve, druge, odnosno treće jednadžbe dodamo a, b, odnosno c, vidimo da vrijedi 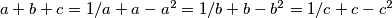
-razmotrimo funkciju 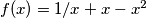 , za koju je očito x različito od nule, imamo
, za koju je očito x različito od nule, imamo 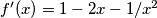 , primijetimo da je
, primijetimo da je 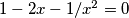 ekvivalentno s
ekvivalentno s 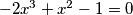
-promotrimo sada funkciju 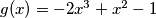 , vrijedi
, vrijedi 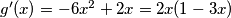 pa su stacionarne točke funkcije g očito
pa su stacionarne točke funkcije g očito 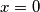 i
i 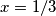
-kako računanjem 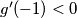 ,
, 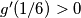 te
te 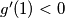 lagano odredimo tok funkcije g te računanjem
lagano odredimo tok funkcije g te računanjem 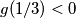 te uspoređivanjem s tokom funkcije zaključujemo da graf funkcije g siječe x-os u najviše jednoj točki, zbog čega funkcija f ima najviše jednu stacionarnu točku, no tada pravac usporedan sa x-osi siječe graf funkcije f u najviše 2 različite točke, zbog čega očito ne mogu svi brojevi a,b,c biti različiti
te uspoređivanjem s tokom funkcije zaključujemo da graf funkcije g siječe x-os u najviše jednoj točki, zbog čega funkcija f ima najviše jednu stacionarnu točku, no tada pravac usporedan sa x-osi siječe graf funkcije f u najviše 2 različite točke, zbog čega očito ne mogu svi brojevi a,b,c biti različiti
 Školjka
Školjka  realni brojevi različiti od nule takvi da vrijedi
realni brojevi različiti od nule takvi da vrijedi 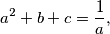
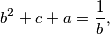
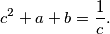 Dokaži da su neka dva od
Dokaži da su neka dva od