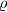
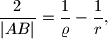
Dvije kružnice jednakog polumjera upisane su u trokut tako da se međusobno dodiruju, te jedna od njih dodiruje stranice i , a druga stranice i . Dokaži da vrijedi gdje je polumjer upisane kružnice trokuta .
%V0
Dvije kružnice jednakog polumjera $\varrho $ upisane su u trokut $ABC$ tako da se međusobno dodiruju, te jedna od njih dodiruje stranice $\overline{AB}$ i $\overline{AC}$, a druga stranice $\overline{AB}$ i $\overline{BC}$. Dokaži da vrijedi $$
\dfrac{2}{|AB|}=\dfrac{1}{\varrho }-\dfrac{1}{r},
$$ gdje je $r$ polumjer upisane kružnice trokuta $ABC$.
Upozorenje: Ovaj zadatak još niste riješili! Kliknite ovdje kako biste prikazali rješenje.
Označimo središta malih kružnića sa i i primjetimo da pravci i prolaze točkom - središto upisane kružnice. Sad uočimo sličnost i Prema kojoj dobijamo Ljeva strana su visine ako nije očito.
I onda dobijemo Što je ista stvar kao i tvrdnja zadatka.
Označimo središta malih kružnića sa $S_1$ i $S_2$ i primjetimo da pravci $AS_1$ i $BS_2$ prolaze točkom $S$ - središto upisane kružnice.
Sad uočimo sličnost $SS_1S_2$ i $SAB$
Prema kojoj dobijamo
$$\frac{2r_1}{|AB|} = \frac{r - r_1}{r}$$
Ljeva strana su visine ako nije očito.
I onda dobijemo
$$\frac{2}{|AB|} = \frac{r - r_1}{rr_1}$$
Što je ista stvar kao i tvrdnja zadatka.
Školjka 
upisane su u trokut 
tako da se međusobno dodiruju, te jedna od njih dodiruje stranice 
i 
, a druga stranice 
. Dokaži da vrijedi 
gdje je 
polumjer upisane kružnice trokuta 
i 
i primjetimo da pravci 
i 
prolaze točkom 
- središto upisane kružnice. Sad uočimo sličnost 
i 
Prema kojoj dobijamo 
Ljeva strana su visine ako nije očito.
Što je ista stvar kao i tvrdnja zadatka.