Točno
19. travnja 2012. 23:01 (13 godine, 10 mjeseci)
Dokažite da za svaki trokut sa stranicama

,

,

i nasuprotnim kutovima

,

,

vrijedi jednakost
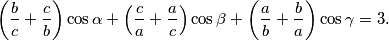
%V0
Dokažite da za svaki trokut sa stranicama $a$, $b$, $c$ i nasuprotnim kutovima $\alpha$, $\beta$, $\gamma$ vrijedi jednakost $$\left( \frac bc + \frac cb \right)\cos \alpha + \left( \frac ca + \frac ac \right)\cos \beta + \left( \frac ab + \frac ba \right)\cos \gamma = 3\text{.}$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Primjenom sinusovog poučka dobivamo
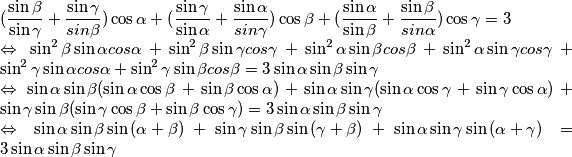
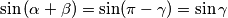
Uvrštavanjem dobivamo
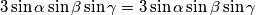
%V0
Primjenom sinusovog poučka dobivamo
$ (\dfrac{\sin{\beta}}{\sin{\gamma}} + \dfrac{\sin{\gamma}}{sin{\beta}})\cos{\alpha} + (\dfrac{\sin{\gamma}}{\sin{\alpha}} + \dfrac{\sin{\alpha}}{sin{\gamma}})\cos{\beta} + (\dfrac{\sin{\alpha}}{\sin{\beta}} + \dfrac{\sin{\beta}}{sin{\alpha}})\cos{\gamma} = 3 \newline \Leftrightarrow \sin^2{\beta}\sin{\alpha}cos{\alpha} + \sin^2{\beta}\sin{\gamma}cos{\gamma} + \sin^2{\alpha}\sin{\beta}cos{\beta} + \sin^2{\alpha}\sin{\gamma}cos{\gamma} + \sin^2{\gamma}\sin{\alpha}cos{\alpha} + \sin^2{\gamma}\sin{\beta}cos{\beta} = 3\sin{\alpha}\sin{\beta}\sin{\gamma} \newline \Leftrightarrow \sin{\alpha}\sin{\beta}(\sin{\alpha}\cos{\beta} + \sin{\beta}\cos{\alpha} ) + \sin{\alpha}\sin{\gamma}(\sin{\alpha}\cos{\gamma} + \sin{\gamma}\cos{\alpha} ) + \sin{\gamma}\sin{\beta}(\sin{\gamma}\cos{\beta} + \sin{\beta}\cos{\gamma} ) = 3\sin{\alpha}\sin{\beta}\sin{\gamma} \newline \Leftrightarrow \sin{\alpha}\sin{\beta}\sin{(\alpha + \beta)} + \sin{\gamma}\sin{\beta}\sin{(\gamma + \beta)} + \sin{\alpha}\sin{\gamma}\sin{(\alpha + \gamma)} = 3\sin{\alpha}\sin{\beta}\sin{\gamma} $
$ \sin{(\alpha + \beta)}=\sin({\pi - \gamma)} = \sin{\gamma} $
Uvrštavanjem dobivamo
$ 3\sin{\alpha}\sin{\beta}\sin{\gamma} = 3\sin{\alpha}\sin{\beta}\sin{\gamma} $
| 20. travnja 2012. 17:22 | mljulj | Točno |