Neocijenjeno
19. veljače 2023. 00:02 (3 godine)
Odredi sve trojke pozitivnih realnih brojeva 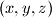 takve da vrijedi
takve da vrijedi 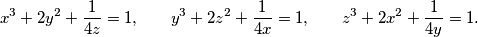
Odredi sve trojke pozitivnih realnih brojeva $(x, y, z)$ takve da vrijedi
$$
x^3 + 2y^2 + \frac{1}{4z} = 1 \text{,} \quad\quad
y^3 + 2z^2 + \frac{1}{4x} = 1 \text{,} \quad\quad
z^3 + 2x^2 + \frac{1}{4y} = 1 \text{.}
$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Primjetimo da je sustav simetričan.
Tako da možemo pretpodstaviti $$x \geq max(y , z)$$
Preko
$$x^3 + \frac{1}{4z} + 2y^2 = y^3 + \frac{1}{4x} + 2z^2$$
Iz
$$x^3 + \frac{1}{4z} \geq y^3 + \frac{1}{4x}$$
Zaključujemo
$$z \geq y$$
A iz
$$y^3 + 2z^2 + \frac{1}{4x} = z^3 + 2x^2 + \frac{1}{4y} $$
Imamo $$ y \geq z$$
Od tu imamo $$y = z$$
Sad radi
$$x^3 \geq y^3$$
$$\frac{1}{4z} \geq \frac{1}{4x}$$
Po što je zbroj te dvi nejednakosti jednak onda imamo
$$x = y = z$$
Sad imamo
$$4x^4 + 8x^3 -4x + 1=0$$
Ovo ima rješenja $$(\sqrt{3} - 1)/2$$ nakon faktorizacije koje se niko nebi sitia