Neocijenjeno
16. svibnja 2023. 16:31 (1 godina, 9 mjeseci)
U ravnini je dano pet točaka
,
,
,
,
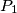
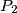
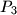
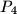
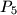
sa cjelobrojnim koordinatama. Pokažite da postoji bar jedan par
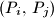
za
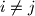
tako da pravac
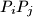
sadrži neku točku
sa cjelobrojnim koordinatama koja leži između
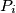
i
.
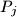
%V0
U ravnini je dano pet točaka $P_1$, $P_2$, $P_3$, $P_4$, $P_5$ sa cjelobrojnim koordinatama. Pokažite da postoji bar jedan par $(P_i,\,P_j)$ za $i \neq j$ tako da pravac $P_iP_j$ sadrži neku točku $Q$ sa cjelobrojnim koordinatama koja leži između $P_i$ i $P_j$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Činjenica :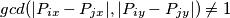 
ako i samo ako za te točke 
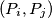vrijedi tvrdnja zadatka.
(Ovo sam dokazao preko sličnosti)
Gledamo kordinate točaka mod 2. Imamo 4 ostatka i 5 brojeva. Time vidimo da između 5 točaka najveći zajednički dijelitelj neke dvije bit će minimalno 2.
Činjenica : $gcd(|P_{ix} - P_{jx}| , |P_{iy} - P_{jy}|) \neq 1$ ako i samo ako za te točke $(P_i , P_j)$ vrijedi tvrdnja zadatka.
(Ovo sam dokazao preko sličnosti)
Gledamo kordinate točaka mod 2. Imamo 4 ostatka i 5 brojeva. Time vidimo da između 5 točaka najveći zajednički dijelitelj neke dvije bit će minimalno 2.
Školjka