Neocijenjeno
16. svibnja 2023. 17:57 (2 godine, 9 mjeseci)
Dokažite da među svakih
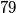
uzastopnih prirodnih brojeva postoji barem jedan čija je suma znamenaka djeljiva sa

.
Nađite niz od
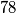
uzastopnih prirodnih brojeva sa svojstvom da suma znamenaka niti jednog od njih nije djeljiva sa

.
%V0
Dokažite da među svakih $79$ uzastopnih prirodnih brojeva postoji barem jedan čija je suma znamenaka djeljiva sa $13$.
Nađite niz od $78$ uzastopnih prirodnih brojeva sa svojstvom da suma znamenaka niti jednog od njih nije djeljiva sa $13$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Prvi dio. Ako su zadnje dvi znamenke 61 ili veće onda dodamo 39 i onda možemo dodati tom broju neki broj od 0 do 39 tako da ostatak bude 0 mod 13.
Ako su zadnje dvi znamenke 60 ili manje. Dodamo neki broj da znamenka jedinica bude 0. sad možemo dodavat znamenki jedinica i desetici brojeve da zbroj bude 0 mod 13. Trebamo max dodat 39.
Primjer Brojevi od 9999999961 do 9999999961 + 77
Razlog - moj "algoritam"
Prvi dio. Ako su zadnje dvi znamenke 61 ili veće onda dodamo 39 i onda možemo dodati tom broju neki broj od 0 do 39 tako da ostatak bude 0 mod 13.
Ako su zadnje dvi znamenke 60 ili manje. Dodamo neki broj da znamenka jedinica bude 0. sad možemo dodavat znamenki jedinica i desetici brojeve da zbroj bude 0 mod 13. Trebamo max dodat 39.
Primjer
Brojevi od 9999999961 do 9999999961 + 77
Razlog - moj "algoritam"
 Školjka
Školjka 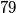 uzastopnih prirodnih brojeva postoji barem jedan čija je suma znamenaka djeljiva sa
uzastopnih prirodnih brojeva postoji barem jedan čija je suma znamenaka djeljiva sa  .
.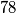 uzastopnih prirodnih brojeva sa svojstvom da suma znamenaka niti jednog od njih nije djeljiva sa
uzastopnih prirodnih brojeva sa svojstvom da suma znamenaka niti jednog od njih nije djeljiva sa