Rješenja zadatka "Školsko/gradsko natjecanje iz matematike 2015, SŠ3 A 5" korisnika "Patrlk"

Neocijenjeno

19. studenoga 2023. 23:59 (5 mjeseci)

Korisnik: Patrlk
Zadatak: Školsko/gradsko natjecanje iz matematike 2015, SŠ3 A 5 (Sakrij tekst zadatka)

Odredi najmanji prirodni broj $n$ takav da u svakom skupu koji se sastoji od $n$ cijelih brojeva postoje tri međusobno različita elementa $a$ , $b$ i $c$ takva da je $ab + bc + ca$ djeljivo s $3$ .

Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.

6. Gledamo ostatke , ne brojeve

Ostatci (1 , 1 , 2 , 2 ,3 ) su primjer 5 brojeva za koje 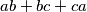$ab + bc + ca$ nikad neće bit djeljivo s 3. Sad dokažimo da za 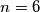$n = 6$ ovo vrijedi.

Za 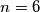$n = 6$ imamo dva slucaja Postoje $2$ broja koja su djeljiva s $3$ Postoje $3$ broja s istim ostatkom

U oba slucana te brojeve možemo uvrstit i dobit ćemo broj koji je djeljiv s $3$ .

Školjka