Neocijenjeno
7. rujna 2023. 14:27 (1 godina, 3 mjeseci)
Neka je
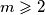
prirodan broj. Koliko rješenja u skupu prirodnih brojeva ima jednadžba
(
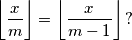
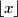
je oznaka za najveći cijeli broj koji nije veći od
.)
%V0
Neka je $m \geqslant 2$ prirodan broj. Koliko rješenja u skupu prirodnih brojeva ima jednadžba $$\left\lfloor{\vphantom{\frac{x}{m-1}}\frac{x}{m}}\right\rfloor = \left\lfloor{\frac{x}{m-1}}\right\rfloor \text{?}$$
($\left\lfloor x \right\rfloor$ je oznaka za najveći cijeli broj koji nije veći od $x$.)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Ako stavimo da je $x = m(m - 1)k + n$
Dobijemo
$$\left\lfloor \frac{n}{m} \right\rfloor - \left\lfloor \frac{n}{m - 1}\right\rfloor = k < 1$$
$x = n < m(m - 1)$
Očito vrijedi da je x između
$$\left< 1 , (m - 1) - 1 \right>$$
$$\left<m , 2(m - 1) - 1 \right>$$
$$...$$
$$\left<m(m - 2) , (m - 1)^2 - 1 \right>$$
Tako da tih brojeva ima
$$\left(\sum_{i = 1}^{m - 1} i(m - 1) - 1 \right) - \left(\sum_{k = 1}^{m - 2} km \right) + m - 2$$
Ili ti $$\frac{m(m + 1)}{2}$$
Školjka 
Dobijemo 
