Neocijenjeno
7. rujna 2023. 21:24 (1 godina, 3 mjeseci)
Neka je
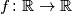
kvadratna funkcija
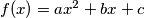
. Označimo sa
diskriminantu, sa
umnožak, a sa
zbroj njezinih nultočaka. Pokažite da postoji samo jedna funkcija
za koju su
,
,
,
četiri uzastopna cijela broja (u rastućem poretku).
%V0
Neka je $f \colon \mathbb{R} \to \mathbb{R}$ kvadratna funkcija $f\!\left(x\right) = ax^2+bx+c$. Označimo sa $D$ diskriminantu, sa $P$ umnožak, a sa $S$ zbroj njezinih nultočaka. Pokažite da postoji samo jedna funkcija $f$ za koju su $a$, $D$, $P$, $S$ četiri uzastopna cijela broja (u rastućem poretku).
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
$$b = -a(a + 3)$$
$$c = a(a + 2)$$
$$D = (a(a + 3))^2 - 4a^2(a + 2) = a + 1$$
$$a | 1$$
$a$ nije $1$
Tako da jedinstvena funkcija
$$f(x) = -x^2 + 2x - 1$$
Školjka 
