Neocijenjeno
8. rujna 2023. 17:49 (1 godina, 2 mjeseci)
a) Dokaži da za međusobno različite prirodne brojeve
i
postoji beskonačno mnogo prirodnih brojeva
takvih da su brojevi
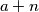
i
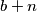
relativno prosti.
b) Postoje li međusobno različiti prirodni brojevi
,
,
i
za koje ne postoji prirodni broj
takav da su brojevi
,
,
,
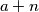
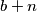
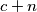
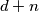
u parovima relativno prosti?
%V0
a) Dokaži da za međusobno različite prirodne brojeve $a$ i $b$ postoji beskonačno mnogo prirodnih brojeva $n$ takvih da su brojevi $a+n$ i $b+n$ relativno prosti.
b) Postoje li međusobno različiti prirodni brojevi $a$, $b$, $c$ i $d$ za koje ne postoji prirodni broj $n$ takav da su brojevi $a+n$, $b+n$, $c+n$, $d+n$ u parovima relativno prosti?
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
$$M(a + n , b + n) = M(a + n , b - a)$$
$b - a$ je neki broj. Nije znanstvena fantastika da $a + n$ može bit $(b - a)k + 1$ za beskonačno mnogo $k$.
b) 1 , 2 , 3 ,4?
Za neparan n su neka dva parna , za paran su opet neka dva parna. Možda nije dobro formulirano pitanje.
Školjka 
je neki broj. Nije znanstvena fantastika da 
može bit 
za beskonačno mnogo 
.