Neocijenjeno
10. rujna 2023. 21:24 (2 godine, 6 mjeseci)
Neka su

i

pozitivni iracionalni brojevi takvi da je
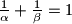
, te
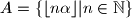
i
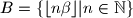
. Dokažite da je tada
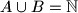
i
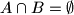
.
Naputak: Možete dokazati ekvivalentnu tvrdnju: Za funkciju
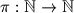
definiranu sa
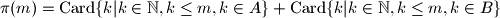
vrijedi
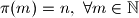
.
(
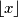
je oznaka za najveći cijeli broj koji nije veći od

.)
%V0
Neka su $\alpha$ i $\beta$ pozitivni iracionalni brojevi takvi da je $\frac1\alpha + \frac1\beta = 1$, te $A=\{\lfloor n\alpha \rfloor | n \in \mathbb{N}\}$ i $B=\{\lfloor n\beta \rfloor | n \in \mathbb{N}\}$. Dokažite da je tada $A \cup B = \mathbb{N}$ i $A \cap B = \emptyset$.
Naputak: Možete dokazati ekvivalentnu tvrdnju: Za funkciju $\pi : \mathbb{N} \rightarrow \mathbb{N}$ definiranu sa
$$\pi(m)=\mathrm{Card} \{k | k \in \mathbb{N}, k \leq m, k \in A\} + \mathrm{Card} \{k | k \in \mathbb{N}, k \leq m, k \in B\}$$ vrijedi $\pi(m)=n, \,\, \forall m \in \mathbb{N}$.
( $\lfloor x \rfloor$ je oznaka za najveći cijeli broj koji nije veći od $x$.)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Prvo. Najmanji od ta dva je
$$1 + p , \ p \in \mathbb{I} , p \in \left<0 , 1\right>$$
A najveći je
$$1 + \frac{1}{p}$$
Tako da imamo
$$A = \{a + \left\lfloor ap \right\rfloor \ | \ a \in \mathbb{N} \}$$
$$B = \{a + \left\lfloor \frac{a}{p} \right\rfloor \ | \ a \in \mathbb{N} \}$$
Važno je naglasit da su oba skupa rastuća. Tjst veći $a$ veći broj.
Ajmo prvo dokazat da nikoji broj nije u oba skupa.
Ajmo reć da je $n$ u skupu $A$
$$n = a + \lfloor ap \rfloor$$
$$n - a + 1 > ap > n - a$$
$$\frac{n - a + 1}{p} > a > \frac{n - a}{p}$$
Onda je
$$n - a + \left\lfloor \frac{n - a}{p} \right\rfloor < n$$
$$n - a + 1 + \left\lfloor \frac{n - a + 1}{p} \right\rfloor > n$$
Zato što je skup $B$ rastuć. Ne može biti $n$ u tom skupu.
Analogno dokažemo ako je $n$ u $B$ da nije u $A$.
Sad da dokažemo da je svaki broj ili u skupu $A$ ili $B$
Ajmo pretpodstaviti da $n$ nije u skupu $A$
Onda imamo
$$n + \lfloor np \rfloor > n \ , \ np > 1$$
Sad za
$$n - 1 \lfloor (n - 1)p \rfloor$$
Imamo $2$ opcije.
$$(n - 1)p < 1$$
Ili
$$(n - 1)p > 2$$
Za prvu opciju vrijedi
$$n - 1 < \frac{1}{p} < n$$
Što bi znaćilo da je $$1 + \left\lfloor \frac{1}{p} \right\rfloor = n$$
Za drugu opciju opet dobijamo $2$ opcije
$$(n - 2)p < 2$$
$$(n - 2)p > 3$$
Ako vrijedi prva opcija onda je $n$ u drugom skupu.
To možemi zaključit ako je
$$(n - b + 1)p > b$$
i
$$(n - b)p < b$$
Onda je
$$n - b < \frac{b}{p} < n - b + 1$$
Pa je zato ako ikad vrijedi prva obcija $n$ je u skupu $B$
Ali prije ili kasnije će biti
$$(n - b)p > b + 1$$
Gdje će $(n - b) \leq b + 1$ pa će prva opcija vrijedit.
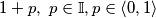 A najveći je
A najveći je 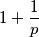
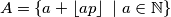
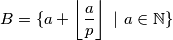
 veći broj. Ajmo prvo dokazat da nikoji broj nije u oba skupa. Ajmo reć da je
veći broj. Ajmo prvo dokazat da nikoji broj nije u oba skupa. Ajmo reć da je  u skupu
u skupu 
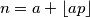
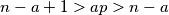
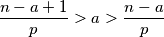 Onda je
Onda je 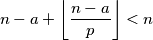
 Zato što je skup
Zato što je skup  rastuć. Ne može biti
rastuć. Ne može biti  u tom skupu.
u tom skupu. u
u  da nije u
da nije u  .
. ili
ili  Ajmo pretpodstaviti da
Ajmo pretpodstaviti da  nije u skupu
nije u skupu  Onda imamo
Onda imamo 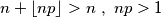 Sad za
Sad za 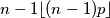 Imamo
Imamo  opcije.
opcije. 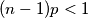 Ili
Ili 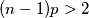 Za prvu opciju vrijedi
Za prvu opciju vrijedi 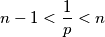 Što bi znaćilo da je
Što bi znaćilo da je 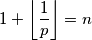
 opcije
opcije 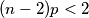
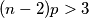 Ako vrijedi prva opcija onda je
Ako vrijedi prva opcija onda je  u drugom skupu.
u drugom skupu.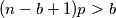 i
i 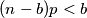 Onda je
Onda je 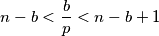
 je u skupu
je u skupu 
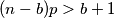 Gdje će
Gdje će 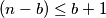 pa će prva opcija vrijedit.
pa će prva opcija vrijedit.  Školjka
Školjka  i
i  pozitivni iracionalni brojevi takvi da je
pozitivni iracionalni brojevi takvi da je 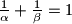 , te
, te 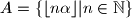 i
i 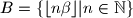 . Dokažite da je tada
. Dokažite da je tada 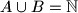 i
i 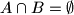 .
.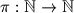 definiranu sa
definiranu sa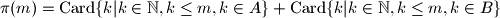 vrijedi
vrijedi 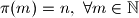 .
.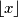 je oznaka za najveći cijeli broj koji nije veći od
je oznaka za najveći cijeli broj koji nije veći od  .)
.)