Kliknite ovdje kako biste prikazali rješenje.
Ajmo prvo koristit indukciju da dokažemi da vrijedi za sve 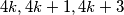 i nazivat ćemo te brojeve na ploči niz.
i nazivat ćemo te brojeve na ploči niz.
Pretpostavka : Pretpodstavimo da vrijedi za neki 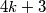 tako da je svaki broj niza na kraju procesa jednak
tako da je svaki broj niza na kraju procesa jednak 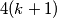 Tjst taj niz se može zapisat :
Tjst taj niz se može zapisat : 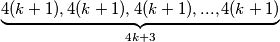
Onda će i ta pretpostavka radit za 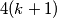 jer niz
jer niz 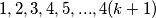 Možemo pretvorit u
Možemo pretvorit u 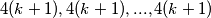 Iz dane pretpostavke. Svaki broj tog niza bit će
Iz dane pretpostavke. Svaki broj tog niza bit će 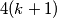
Sad pretpodstavimo da za neki 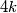 gdje se svaki broj iz tog niza može postupkom dobit da je
gdje se svaki broj iz tog niza može postupkom dobit da je 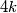 Tjst taj niz bi bio :
Tjst taj niz bi bio : 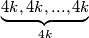
Onda niz 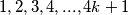 Možemo postupkom doć do :
Možemo postupkom doć do : 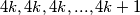 Brojeva
Brojeva 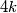 ima parno tako da ako dodajemo 1 u parovima postić ćemo niz :
ima parno tako da ako dodajemo 1 u parovima postić ćemo niz : 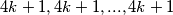 Svaki broj tog niza je
Svaki broj tog niza je 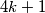
Sad pretpodstavimo da za neki 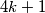 možemo postić da svi brojevi budu
možemo postić da svi brojevi budu 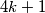
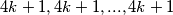 Onda za niz
Onda za niz 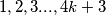 Možemo ga zapisat kao
Možemo ga zapisat kao 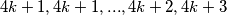 Dodadavanje jedinice prvom i zadnjem , prvom i predzadjen , i dvice ovima u parovima dobijamo niz
Dodadavanje jedinice prvom i zadnjem , prvom i predzadjen , i dvice ovima u parovima dobijamo niz 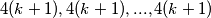 Svaki broj tog niza je
Svaki broj tog niza je 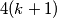
Iz 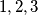 može se postić
može se postić 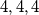 tako da svi brojevi osim
tako da svi brojevi osim 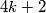 padaju ko domine.
padaju ko domine.
Sad dokaz da 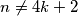 Ograničimo Ante da miže dodavat samo broj
Ograničimo Ante da miže dodavat samo broj  ako oće dodavat broj veći od
ako oće dodavat broj veći od  dodat će broj
dodat će broj  više puta.
više puta.
Uglavnom to nije ni toliko važno. Ali dodavanje  na
na  parna broja. Broj parnih brojeva se smanjuje za
parna broja. Broj parnih brojeva se smanjuje za  Dodavanje
Dodavanje  na neparne povećaje se za
na neparne povećaje se za  i dodavanje na miks broj parnih brojeva ostaje isti. Na početku broj parnih brojeva je
i dodavanje na miks broj parnih brojeva ostaje isti. Na početku broj parnih brojeva je 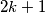 A može se povećavat samo za
A može se povećavat samo za  ili smanjit za
ili smanjit za  tako da jedine vrijednosti koje može postić je
tako da jedine vrijednosti koje može postić je 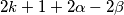 Tojest
Tojest 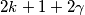 Vidimo da je broj parnih brojeva strogo neparan. Što je kontradikcija tome da svi brojevi trebaju biti isti (u tom slucaju je broj neparnih brojeva ili
Vidimo da je broj parnih brojeva strogo neparan. Što je kontradikcija tome da svi brojevi trebaju biti isti (u tom slucaju je broj neparnih brojeva ili  ili
ili 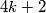 )
)
Edit : mislio sam da sam loš u indukciji da pišem ovoliko dugo rješenja. Očito samo neznam konstrukciju
 Školjka
Školjka  prirodnih brojeva (
prirodnih brojeva (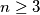 ). Ante ponavlja sljedeći postupak: najprije po volji bira dva broja na ploči, a zatim ih povećava za isti proizvoljni iznos.
). Ante ponavlja sljedeći postupak: najprije po volji bira dva broja na ploči, a zatim ih povećava za isti proizvoljni iznos.