Školjka Neocijenjeno
30. rujna 2023. 14:28 (1 godina, 5 mjeseci)
Na natjecanju je bilo 
strijelaca. Svaki natjecatelj gađa 
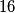puta metu koja je podijeljena na dva dijela, A i B. Ako pogodi u dio A natjecatelj dobiva 
bodova, a ako pogodi u dio B dobiva 
bodova. Na kraju natjecanja utvrđeno je da je broj pogodaka u dio B veći od polovine ukupnog broja odapetih strelica te da je ukupan broj promašaja jednak ukupnom broju pogodaka u dio A.
Dokaži da su barem dva natjecatelja ostvarila isti broj bodova.
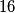strijelaca. Svaki natjecatelj gađa puta metu koja je podijeljena na dva dijela, A i B. Ako pogodi u dio A natjecatelj dobiva bodova, a ako pogodi u dio B dobiva bodova. Na kraju natjecanja utvrđeno je da je broj pogodaka u dio B veći od polovine ukupnog broja odapetih strelica te da je ukupan broj promašaja jednak ukupnom broju pogodaka u dio A.Dokaži da su barem dva natjecatelja ostvarila isti broj bodova.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Oznaćimo s 
broj pogodaka u dio 
a , 
broj pogodaka u dio 
i broj promašaja.
Iz ovih uvjeta imamo :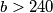
, 
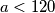Zato što je 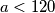a brojevi 
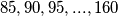Imaju minimalno 
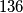pogodaka u što znaći da ćemo trebat izbacit barem 
. I analogno od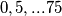 
Ćemo trebat izbacit barem radi istog razloga. Sad nam ostaje samo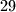 
broja koji strijelci mogu postić. A ima strijelaca