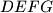
U pravokutni trokut s duljinom hipotenuze i pripadnom visinom upisan je kvadrat sa dva susjedna vrha , na hipotenuzi i po jednim vrhom i na katetama i . Izračunajte duljinu stranice tog kvadrata i dokažite jednakost .
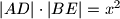
%V0
U pravokutni trokut $ABC$ s duljinom hipotenuze $c$ i pripadnom visinom $h$ upisan je kvadrat $DEFG$ sa dva susjedna vrha $D$, $E$ na hipotenuzi $\overline{AB}$ i po jednim vrhom $F$ i $G$ na katetama $\overline{BC}$ i $\overline{CA}$. Izračunajte duljinu $x$ stranice tog kvadrata i dokažite jednakost $\left\vert AD \right\vert \cdot \left\vert BE \right\vert = x^2$.
Upozorenje: Ovaj zadatak još niste riješili! Kliknite ovdje kako biste prikazali rješenje.
Iz slićnosti slijedi 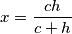Druga jednakost slijedi iz slićnosti.
Iz slićnosti slijedi
$$x=\frac{ch}{c + h}$$
Druga jednakost slijedi iz slićnosti.
Školjka 
s duljinom hipotenuze 
i pripadnom visinom 
upisan je kvadrat 
sa dva susjedna vrha 
, 
na hipotenuzi 
i po jednim vrhom 
i 
na katetama 
i 
. Izračunajte duljinu 
stranice tog kvadrata i dokažite jednakost 
. 
Druga jednakost slijedi iz slićnosti.