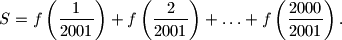Neocijenjeno
16. prosinca 2023. 14:23 (2 godine, 2 mjeseci)
Dana je funkcija
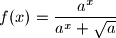
, gdje je

pozitivan realan broj. Odredite
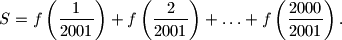
%V0
Dana je funkcija $f(x)=\displaystyle{\frac{a^x}{a^x+\sqrt{a}}}$, gdje je $a$ pozitivan realan broj. Odredite $$
S=f\left(\frac{1}{2001}\right)+f\left(\frac{2}{2001}\right)+ \ldots +
f\left(\frac{2000}{2001}\right).
$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Izračunajmo vrijednosti funkcija koje čine sumu:
$$S = \frac{a^{\frac{1}{2001}}}{a^{\frac{1}{2001}}+\sqrt{a}} + \frac{a^{\frac{2}{2001}}}{a^{\frac{2}{2001}}+\sqrt{a}} + ... + \frac{a^{\frac{1999}{2001}}}{a^{\frac{1999}{2001}}+\sqrt{a}}+ \frac{a^{\frac{2000}{2001}}}{a^{\frac{2000}{2001}}+\sqrt{a}}$$
Promotrimo li eksponente, gledajući "od nazad" sumu, vidjet ćemo da vrijedi: $\frac{2000}{2001} = 1 - \frac{1}{2001}$, $\frac{1999}{2001} = 1 - \frac{2}{2001}$ itd. Uvrstimo:
$$S = \frac{a^{\frac{1}{2001}}}{a^{\frac{1}{2001}}+\sqrt{a}} + \frac{a^{\frac{2}{2001}}}{a^{\frac{2}{2001}}+\sqrt{a}} + ... + \frac{a^{1-\frac{2}{2001}}}{a^{1-\frac{2}{2001}}+\sqrt{a}}+ \frac{a^{1-\frac{1}{2001}}}{a^{1-\frac{1}{2001}}+\sqrt{a}}$$
$$S = \frac{a^{\frac{1}{2001}}}{a^{\frac{1}{2001}}+\sqrt{a}} + \frac{a^{\frac{2}{2001}}}{a^{\frac{2}{2001}}+\sqrt{a}} + ... + \frac{a^{1}\cdot a^{-\frac{2}{2001}}}{a^{1}\cdot a^{-\frac{2}{2001}} + \sqrt{a}} + \frac{a^{1}\cdot a^{-\frac{1}{2001}}}{a^{1}\cdot a^{-\frac{1}{2001}} + \sqrt{a}}$$
$$S = \frac{a^{\frac{1}{2001}}}{a^{\frac{1}{2001}}+\sqrt{a}} + \frac{a^{\frac{2}{2001}}}{a^{\frac{2}{2001}}+\sqrt{a}} + ... + \frac{\frac{a}{a^{\frac{2}{2001}}}}{\frac{a}{a^{\frac{2}{2001}}} + \sqrt{a}}+\frac{\frac{a}{a^{\frac{1}{2001}}}}{\frac{a}{a^{\frac{1}{2001}}} + \sqrt{a}}$$
Valja se prisjetiti da se može zapisati $a = \sqrt{a} \cdot \sqrt{a}$, a onda primijetiti da se razlomci (gledajući "od nazad") mogu podijeliti s $\sqrt{a}$ ($a>0$ prema uvjetu).
$$S = \frac{a^{\frac{1}{2001}}}{a^{\frac{1}{2001}}+\sqrt{a}} + \frac{a^{\frac{2}{2001}}}{a^{\frac{2}{2001}}+\sqrt{a}} + ... + \frac{\frac{\sqrt{a}}{a^{\frac{2}{2001}}}}{\frac{\sqrt{a}}{a^{\frac{2}{2001}}} + 1}+\frac{\frac{\sqrt{a}}{a^{\frac{1}{2001}}}}{\frac{\sqrt{a}}{a^{\frac{1}{2001}}} + 1}$$
$$S = \frac{a^{\frac{1}{2001}}}{a^{\frac{1}{2001}}+\sqrt{a}} + \frac{a^{\frac{2}{2001}}}{a^{\frac{2}{2001}}+\sqrt{a}} + ... + \frac{\frac{\sqrt{a}}{a^{\frac{2}{2001}}}}{\frac{\sqrt{a}}{a^{\frac{2}{2001}}} + 1}+\frac{\frac{\sqrt{a}}{a^{\frac{1}{2001}}}}{\frac{\sqrt{a}}{a^{\frac{1}{2001}}} + 1}$$
Sredimo zadnje članove sume (i analogne ostale koji se također mogu srediti): $\frac{\frac{\sqrt{a}}{a^{\frac{1}{2001}}}}{\frac{\sqrt{a}+a^{\frac{1}{2001}}}{a^{\frac{1}{2001}}}} = \frac{\sqrt{a}}{a^{\frac{1}{2001}}+\sqrt{a}}$. Suma poprima oblik:
$$S = \frac{a^{\frac{1}{2001}}}{a^{\frac{1}{2001}}+\sqrt{a}} + \frac{a^{\frac{2}{2001}}}{a^{\frac{2}{2001}}+\sqrt{a}} + ... + \frac{\sqrt{a}}{a^{\frac{2}{2001}}+\sqrt{a}}+ \frac{\sqrt{a}}{a^{\frac{1}{2001}}+\sqrt{a}}.$$
Grupirajmo prvi i zadnji, drugi i predzadnji član, ... i dobijemo:
$$S = (\frac{a^{\frac{1}{2001}}}{a^{\frac{1}{2001}}+\sqrt{a}} +\frac{\sqrt{a}}{a^{\frac{1}{2001}}+\sqrt{a}}) + (\frac{a^{\frac{2}{2001}}}{a^{\frac{2}{2001}}+\sqrt{a}}+ \frac{\sqrt{a}}{a^{\frac{2}{2001}}+\sqrt{a}}) + ...$$
$$S = \frac{a^{\frac{1}{2001}}+ \sqrt{a}}{a^{\frac{1}{2001}}+\sqrt{a}} + \frac{a^{\frac{2}{2001}}+\sqrt{a}}{a^{\frac{2}{2001}}+\sqrt{a}} + ...$$
$$S = 1 + 1 + ... $$
Imamo 2000 članova, ali svaki par u zbroju daje jedan što znači da ukupno imamo 1000 jedinica, tj. suma izraza jednaka je: $S = 1000$.
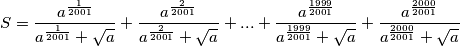 Promotrimo li eksponente, gledajući "od nazad" sumu, vidjet ćemo da vrijedi:
Promotrimo li eksponente, gledajući "od nazad" sumu, vidjet ćemo da vrijedi: 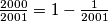 ,
, 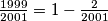 itd. Uvrstimo:
itd. Uvrstimo: 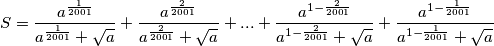
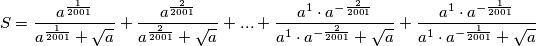
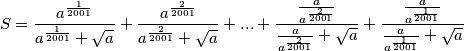 Valja se prisjetiti da se može zapisati
Valja se prisjetiti da se može zapisati 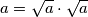 , a onda primijetiti da se razlomci (gledajući "od nazad") mogu podijeliti s
, a onda primijetiti da se razlomci (gledajući "od nazad") mogu podijeliti s 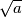 (
(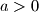 prema uvjetu).
prema uvjetu). 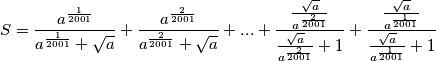
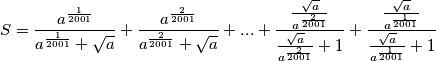 Sredimo zadnje članove sume (i analogne ostale koji se također mogu srediti):
Sredimo zadnje članove sume (i analogne ostale koji se također mogu srediti): 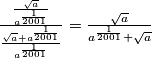 . Suma poprima oblik:
. Suma poprima oblik: 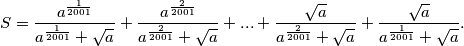 Grupirajmo prvi i zadnji, drugi i predzadnji član, ... i dobijemo:
Grupirajmo prvi i zadnji, drugi i predzadnji član, ... i dobijemo: 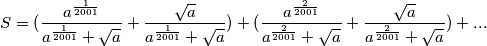
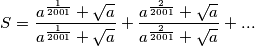
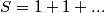 Imamo 2000 članova, ali svaki par u zbroju daje jedan što znači da ukupno imamo 1000 jedinica, tj. suma izraza jednaka je:
Imamo 2000 članova, ali svaki par u zbroju daje jedan što znači da ukupno imamo 1000 jedinica, tj. suma izraza jednaka je: 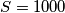 .
.  Školjka
Školjka 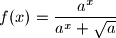 , gdje je
, gdje je  pozitivan realan broj. Odredite
pozitivan realan broj. Odredite