Neocijenjeno
8. siječnja 2024. 18:02 (3 mjeseci, 3 tjedna)
Determine all pairs
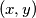
of integers such that
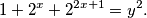
%V0
Determine all pairs $(x, y)$ of integers such that $$1+2^{x}+2^{2x+1}= y^{2}.$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Svako rješenje koje sam vidio mi je bilo malo glupo. Pa evo jedna ljepa alternativa. Množenjem s $4$ dobijamo :
\[4 + 4\cdot 2^x + 8\cdot 2^{2x} = y^2\]
\[7\cdot 2^{2x} + (2^x + 2)^2 = 4y^2\]
\[7 \cdot 2^{2x} = 4(y - 2^{x - 1} - 1)(y + 2^{x - 1} + 1)\]
Barem jedna zagrada dijeli $14$ a obe su djeljive s $2$ za $x - 1 > 0$
Casework na slućajeve i dobijemo rješenje $(4 , \pm 23)$
Dok za $x - 1 < 1$ imamo trivijalan $(0 , \pm 2)$
Školjka 
dobijamo :
a obe su djeljive s 
za 
Dok za 
imamo trivijalan 