Točno
7. rujna 2024. 03:03 (1 godina, 5 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka 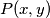 označava danu funkcijsku jednadžbu. Uvrštavanjem dobivamo:
označava danu funkcijsku jednadžbu. Uvrštavanjem dobivamo:
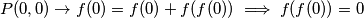
Neka je 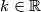 tako da
tako da 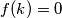 i
i 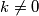
Uvrštavanjem dobivamo:
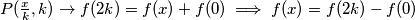
Znači, funkcija  je konstanta, pa uvrštavanjem
je konstanta, pa uvrštavanjem 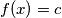 dobivamo da za svaki
dobivamo da za svaki 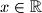 vrijedi
vrijedi 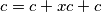 Iz čega očito slijedi
Iz čega očito slijedi 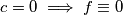 , što je jedno rješenje.
, što je jedno rješenje.
U drugom slučaju imamo 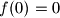
Uvrštavajući imamo:
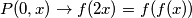
što nam daje motivaciju da dokažemo da je  injektiva. Zaista, pretpostavimo
injektiva. Zaista, pretpostavimo 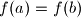 za neke
za neke 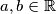 tako da
tako da 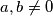 . Uvrštavajući sljedeće vrijednosti dobivamo:
. Uvrštavajući sljedeće vrijednosti dobivamo:
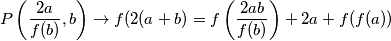
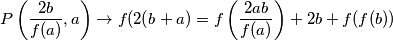
Pa slijedi
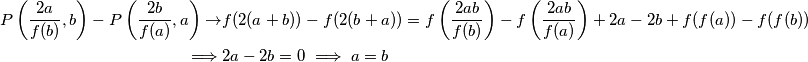
Znači, funkcija je injektivna, iz čega slijedi 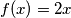 .
.
Sva rješenja su 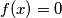 i
i 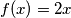 za sve
za sve 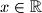 .
.
Provjerom utvrđujemo da to jesu rješenja. Najsss!
 Školjka
Školjka 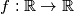 takve da
takve da 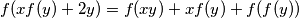 vrijedi za sve realne brojeve
vrijedi za sve realne brojeve  i
i  .
.