Točno
16. rujna 2024. 17:06 (1 godina, 5 mjeseci)
Let
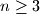
be an integer, and let
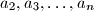
be positive real numbers such that
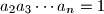
. Prove that
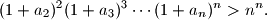
Proposed by Angelo Di Pasquale, Australia
%V0
Let $n\ge 3$ be an integer, and let $a_2,a_3,\ldots ,a_n$ be positive real numbers such that $a_{2}a_{3}\cdots a_{n}=1$. Prove that
$$(1 + a_2)^2 (1 + a_3)^3 \dotsm (1 + a_n)^n > n^n.$$
Proposed by Angelo Di Pasquale, Australia
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
za svaki ai mozemo napisati njegov dio kao: (1+ai)^i= ((1/i-1)+(1/i-1)+(1/i-1)...+(1/i-1)+ai)^i>=(AG) i^i*ai*(i-1)^(1-i) sada množenjem svih ovih članova vidimo da se krate i^i i (i-1)^(1-i) osim prvog i zadnjeg odnosno ostane (1/1)^1 i n^n pa imamo a2a3...an*n^n=n^n sada jos moramo dokazati da ne vrijedi jednakost pa pretpostavimo suprotno tada za svaki put kad smo primjenili ag mora vrijediti jednakost što je jedino moguće ako su svi članovi jednaki pa bi onda ai bio 1/i-1, no kako je svaki član nakon a2 manji od 1 a a2 je jednak jedan tada uvijet zadatka nije ispunjen
za svaki ai mozemo napisati njegov dio kao: (1+ai)^i= ((1/i-1)+(1/i-1)+(1/i-1)...+(1/i-1)+ai)^i>=(AG) i^i*ai*(i-1)^(1-i) sada množenjem svih ovih članova vidimo da se krate i^i i (i-1)^(1-i) osim prvog i zadnjeg odnosno ostane (1/1)^1 i n^n pa imamo a2a3...an*n^n=n^n
sada jos moramo dokazati da ne vrijedi jednakost pa pretpostavimo suprotno tada za svaki put kad smo primjenili ag mora vrijediti jednakost što je jedino moguće ako su svi članovi jednaki pa bi onda ai bio 1/i-1, no kako je svaki član nakon a2 manji od 1 a a2 je jednak jedan tada uvijet zadatka nije ispunjen
| 16. rujna 2024. 20:58 | loki6 | Točno |
 Školjka
Školjka 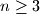 be an integer, and let
be an integer, and let 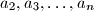 be positive real numbers such that
be positive real numbers such that 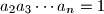 . Prove that
. Prove that