IMO Shortlist 2012 problem A3
Dodao/la:
arhiva3. studenoga 2013. Let
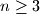
be an integer, and let
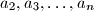
be positive real numbers such that
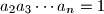
. Prove that
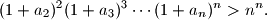
Proposed by Angelo Di Pasquale, Australia
%V0
Let $n\ge 3$ be an integer, and let $a_2,a_3,\ldots ,a_n$ be positive real numbers such that $a_{2}a_{3}\cdots a_{n}=1$. Prove that
$$(1 + a_2)^2 (1 + a_3)^3 \dotsm (1 + a_n)^n > n^n.$$
Proposed by Angelo Di Pasquale, Australia
Izvor: Međunarodna matematička olimpijada, shortlist 2012
Školjka 
