Točno
29. rujna 2024. 19:29 (1 godina, 5 mjeseci)
Korisnik: msaric
Zadatak: Izborno natjecanje 2009 - Izborni test za MEMO: Prvi dan - Zadatak 1 (Sakrij tekst zadatka)
Zadatak: Izborno natjecanje 2009 - Izborni test za MEMO: Prvi dan - Zadatak 1 (Sakrij tekst zadatka)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
 Školjka
Školjka  ,
,  ,
,  i
i  vrijedi
vrijedi 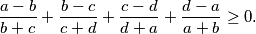
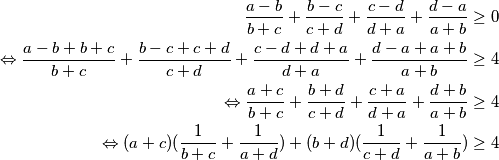 Po Engel formi CSB nejednakosti imamo
Po Engel formi CSB nejednakosti imamo 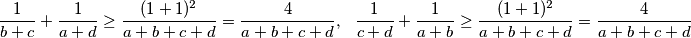 Sad uvrštavanjem dobijemo:
Sad uvrštavanjem dobijemo: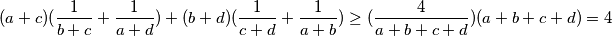
 s
s  u ovoj zadnjoj nejednakosti.
u ovoj zadnjoj nejednakosti.