Zadatak: 1. lakša simulacija državnog natjecanja 2020. zadatak 3 (Sakrij tekst zadatka)
Na ploči je napisano 2020 prirodnih brojeva. Svaku minutu, na ploču dopišemo novi red brojeva na sljedeći način. Ispod svakog broja  u prethodnom redu napišemo broj
u prethodnom redu napišemo broj 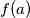 gdje
gdje 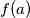 predstavlja broj pojavljivanja broja
predstavlja broj pojavljivanja broja  u prethodnom redu. Dokažite da ćemo u nekom trenutku, jedan za drugim, napisati isti red brojeva.
u prethodnom redu. Dokažite da ćemo u nekom trenutku, jedan za drugim, napisati isti red brojeva.
Kliknite ovdje kako biste prikazali rješenje.
Primijetimo da redoslijed brojeva nije bitan. Broj ispod samo ovisi o broju iznad njega, ne o redoslijedu, tako da su nizovi npr. 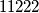 i
i 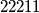 suštinski isti, lakše vidimo ako brojeve rasporedimo u stupce, raspored brojeva u stupcima ovisi isključivo o broju pojavljivanja, ne o redoslijedu. Primijetimo da to znači da brojeve uvijek možemo rasporediti na taj način i da to neće utjecati na naš rezultat. Dakle, bez smanjenja općenitosti možemo pretpostaviti da su svi jednaki brojevi "u skupinama" (tj. niz brojeva može izgledati ovako:
suštinski isti, lakše vidimo ako brojeve rasporedimo u stupce, raspored brojeva u stupcima ovisi isključivo o broju pojavljivanja, ne o redoslijedu. Primijetimo da to znači da brojeve uvijek možemo rasporediti na taj način i da to neće utjecati na naš rezultat. Dakle, bez smanjenja općenitosti možemo pretpostaviti da su svi jednaki brojevi "u skupinama" (tj. niz brojeva može izgledati ovako: 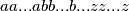 , ovo je samo zbog jednostavnosti; u rješenju čak mislim da nije ni potrebno, ali bar je meni bilo lakše pratiti).
, ovo je samo zbog jednostavnosti; u rješenju čak mislim da nije ni potrebno, ali bar je meni bilo lakše pratiti).
Sada, promotrimo niz gdje su svi brojevi disjunktni. Neka redak prije toga sadrži brojeve 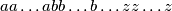 . Tada je redak koji promatramo jednak
. Tada je redak koji promatramo jednak 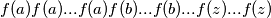 . Kako smo pretpostavili da su svi brojevi disjunktni, slijedi da se broj
. Kako smo pretpostavili da su svi brojevi disjunktni, slijedi da se broj 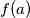 pojavljuje jednak broj puta kao i broj
pojavljuje jednak broj puta kao i broj  u prethodnom retku, dakle promatrani niz bit će identičan onom prethodnom;
u prethodnom retku, dakle promatrani niz bit će identičan onom prethodnom; 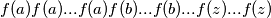 .
.
Nadalje, neka je  ukupan broj različitih brojeva koji se pojavljuju jednak broj puta (tj. za niz
ukupan broj različitih brojeva koji se pojavljuju jednak broj puta (tj. za niz 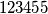 je
je 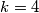 , a za
, a za 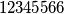 imamo
imamo 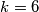 ). Primijetimo da, ako je u nekom trenutku
). Primijetimo da, ako je u nekom trenutku 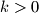 , imamo neki niz međusobno različitih brojeva, recimo
, imamo neki niz međusobno različitih brojeva, recimo 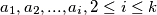 koji se pojavljuju jednak broj puta, dakle
koji se pojavljuju jednak broj puta, dakle 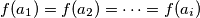 , ako označimo s
, ako označimo s 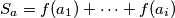 , u idućim redcima slijedit će brojevi
, u idućim redcima slijedit će brojevi 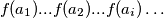
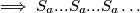 a broj
a broj 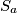 pojavljivat će se
pojavljivat će se 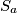 puta. Tada se
puta. Tada se  smanjio za barem
smanjio za barem 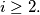 (Možemo zamisliti da su brojevi
(Možemo zamisliti da su brojevi 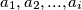 zamijenjeni s
zamijenjeni s 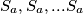 .) Dakle,
.) Dakle,  će se uvijek smanjivati, a kako
će se uvijek smanjivati, a kako 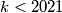 , slijedi da će u nekom trenutku svi brojevi biti različiti (jer se različiti brojevi u prethodnom retku pojavljuju različit broj puta), a pokazali smo da će se u tom trenutku brojevi ponoviti.
, slijedi da će u nekom trenutku svi brojevi biti različiti (jer se različiti brojevi u prethodnom retku pojavljuju različit broj puta), a pokazali smo da će se u tom trenutku brojevi ponoviti.
P.S. Ne znam je li ovo bilo malo nespretno objašnjeno, cijela je ideja bila gledati broj pojavljivanja različitih brojeva, tako da je moguće da su neki djelovi mogli biti malo jasniji.
 Školjka
Školjka