Neocijenjeno
12. travnja 2025. 21:59 (11 mjeseci)
Neka su dani 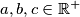 takvi da su svi u parovima različiti. Dokažite da vrijedi
takvi da su svi u parovima različiti. Dokažite da vrijedi
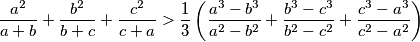
Neka su dani \(a,b,c \in \mathbb{R}^+\) takvi da su svi u parovima različiti. Dokažite da vrijedi
\[\frac{a^2}{a+b}+\frac{b^2}{b+c}+\frac{c^2}{c+a} >\frac{1}{3} \left(\frac{a^3-b^3}{a^2-b^2}+\frac{b^3-c^3}{b^2-c^2}+\frac{c^3-a^3}{c^2-a^2}\right)\]
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
\begin{align*}
&\frac{1}{3} \left(\frac{a^3-b^3}{a^2-b^2}+\frac{b^3-c^3}{b^2-c^2}+\frac{c^3-a^3}{c^2-a^2}\right)\\
&=\frac{1}{3}\left(\sum_{cyc}\frac{(a-b)(a^2+ab+b^2)}{(a-b)(a+b)}\right)\\
&=\frac{1}{3}\left(\sum_{cyc}\frac{a^2+ab+b^2}{a+b}\right)\\
&=\frac{1}{3}\left(\sum_{cyc}\frac{a^2}{a+b}+b\right)\\
&\stackrel{\text{AG}}{\le}\frac{1}{3}\left(\sum_{cyc}\frac{a^2}{a+b}+2\frac{a^2}{a+b}\right)\\
&=\frac{a^2}{a+b}+\frac{b^2}{b+c}+\frac{c^2}{c+a}
\end{align*}
Nejednakost slijedi iz $AG$-a:
$$\sum_{cyc}\left(\frac{a^2}{a+b}+\frac{a+b}{4}\right)\ge \sum_{cyc}a$$
$$\Longleftrightarrow 2\left(\frac{a^2}{a+b}+\frac{b^2}{b+c}+\frac{c^2}{c+a}\right)\ge a+b+c $$
Ako se jednakost postiže, tada imamo
$3a^2=2ab+b^2$\\
$3b^2=2bc+c^2$\\
$3c^2=2ac+a^2$\\
Zbrajajući dobivamo $a^2+b^2+c^2=ab+bc+ca$, što vrijedi akko $a=b=c.\Longrightarrow\Longleftarrow$. Dakle,
$$\frac{a^2}{a+b}+\frac{b^2}{b+c}+\frac{c^2}{c+a} >\frac{1}{3} \left(\frac{a^3-b^3}{a^2-b^2}+\frac{b^3-c^3}{b^2-c^2}+\frac{c^3-a^3}{c^2-a^2}\right)$$