Školjka

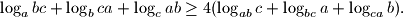
%V0 $\log_a{bc} = \dfrac{\ln bc}{\ln a}=\dfrac{\ln b + \ln c}{\ln a}$ $\log_{bc} a = \dfrac{\ln a}{\ln bc} = \dfrac{\ln a}{\ln b + \ln c}$ $x = \ln a > 0$ $y = \ln b > 0$ $z = \ln c > 0$ $\Rightarrow \displaystyle \sum{\frac{x+y}{z}} \geqslant 4 \sum{\frac{x}{y+z}}$ $\displaystyle \sum{\dfrac{x+y}{2z}} = \sum{\dfrac{\dfrac{x}{y}+\dfrac{x}{z}}{2}} \stackrel{AH}{\geqslant} \sum{\dfrac{2}{\dfrac{y}{x} + \dfrac{z}{x}}} = \sum{\dfrac{2x}{y+z}}$