Točno
3. prosinca 2013. 21:28 (12 godine, 3 mjeseci)
Ako su

,

,

,
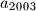
cijeli brojevi i
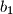
,
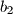
,

,
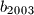
ti isti brojevi poredani na neki drugi način, dokažite da je produkt
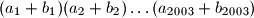
paran broj.
%V0
Ako su $a_1$, $a_2$, $\dots$, $a_{2003}$ cijeli brojevi i $b_1$, $b_2$, $\dots$, $b_{2003}$ ti isti brojevi poredani na neki drugi način, dokažite da je produkt $$
(a_1+b_1)(a_2+b_2) \ldots (a_{2003}+b_{2003})
$$ paran broj.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Primjecujem da broj parnih i broj neparnih ne moze biti jednak jer imamo neparan broj brojeva.
Ako je produkt neparan, onda su

i
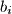
razlicite parnosti, sto bi znacilo da je broj parnih u

jednak broju neparnih u

, sto je jednako broju neparnih u

, dakle kontradikcija.
%V0
Primjecujem da broj parnih i broj neparnih ne moze biti jednak jer imamo neparan broj brojeva.
Ako je produkt neparan, onda su $a_i$ i $b_i$ razlicite parnosti, sto bi znacilo da je broj parnih u $a$ jednak broju neparnih u $b$, sto je jednako broju neparnih u $a$, dakle kontradikcija.
| 5. prosinca 2013. 18:09 | ikicic | Točno |