Točno
3. prosinca 2013. 22:13 (12 godine, 3 mjeseci)
Kvadratna tablica
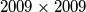
popunjena je brojevima
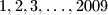
tako da se u svakom retku i svakom stupcu pojavljuje svaki od tih brojeva. Ako je tablica simetrična u odnosu na jednu dijagonalu, onda se i na toj dijagonali pojavljuju svi brojevi
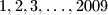
. Dokaži!
%V0
Kvadratna tablica $2009 \times 2009$ popunjena je brojevima $1, 2, 3, \dots, 2009$ tako da se u svakom retku i svakom stupcu pojavljuje svaki od tih brojeva. Ako je tablica simetrična u odnosu na jednu dijagonalu, onda se i na toj dijagonali pojavljuju svi brojevi $1, 2, 3, \dots, 2009$. Dokaži!
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Promatrajmo samo broj

Ako se

ne nalazi na dijagonali, onda znamo da postoji njegov parnjak s druge strane, a posto imamo neparan broj jedinica, mora neparan broj jedinica biti na dijagonali.
Analogno vrijedi za sve ostale brojeve, dakle svi brojevi postoje na dijagonali.
%V0
Promatrajmo samo broj $1$
Ako se $1$ ne nalazi na dijagonali, onda znamo da postoji njegov parnjak s druge strane, a posto imamo neparan broj jedinica, mora neparan broj jedinica biti na dijagonali.
Analogno vrijedi za sve ostale brojeve, dakle svi brojevi postoje na dijagonali.
| 8. siječnja 2014. 16:45 | grga | Točno |