Neocijenjeno
30. svibnja 2014. 23:00 (11 godine, 8 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Unaprijed sory za nepreglednost i dužinu riješenja (ovo je kraća verzija riješenja, bez manjih objašnjenja)
1. Promatramo (mod 3) , iz cega zaključujemo :
2^x*3^y kongurentno 0 (mod 3) i 7^t kongurentno 1 (mod 3) -> 5^z kongruento 1 (mod 3) -> z paran
z = 2*z2
2. Promatramo (mod 8)
1. slucaj , x=1 :
2*3^y kongruento 6 ili 2 (mod 8) *
5^(2*z2) kongruento 1 (mod 8) **
7^t kongruento -1 ili 1 (mod 8) ***
Ovaj sustav ima riješenje samo kada je * kongurento 6 , a *** -1 (mod 8) , pa su y i t neparni.
Sada promatramo (mod 5) u sustavu 2 * 3^( 2*y2 + 1 ) + 5 ^ ( 2*z2 ) = 7^( 2*t2 + 1 )
Vidimo da je prvi član kongurentan 1 ili 4 , a RHS 3 ili 2 (mod 5) , pa zaključujemo da ovaj sustav nema riješenja.
2. slučaj , x = 2 :
4*3^y kongruento 4 (mod 8)
5^(2*z2) kongruento 1 (mod 8)
7^t kongruento -1 ili 1 (mod 8)
Očito , ovaj sustav nema riješenja.
3. slučaj , x >= 3
Sada primjećujemo da 7^t mora biti kongruentno 1 mod 8 , pa je t paran -> t = 2*t2
Kada prebacimo 2. član LHS na desnu stranu dobijemo sljedeći izgled jednadžbe :
2^x * 3^y = (7 ^ t2 - 5 ^ z2) (7 ^ t2 + 5 ^ z2)
U ovoj jednažbi primjećujemo da ako je jedna zagrada RHS-a dijeljiva s 3 , druga nije , a ta koja nije mora biti isključivo potencija broja 2, pa mozemo promatramo 2 slučaja :
1. slučaj 7 ^ t2 - 5 ^ z2 = 2 ^ k
1. 1. : t2 = 1 , z2 = 1 :
riješenja ovoga ispadnu x = 3 , y = 1 , z = 2 , t = 2 , donosno
2^3 * 3 + 5^2 = 7^2
1. 2. !(t2 = 1 & z2 = 1)
Kako je 7 ^ t2 + 5 ^ z2 dijeljivo s 3 , zakljucujemo da je z2 neparan , z2 = 2z3 + 1
Gledamo (mod 8) :
5 ^ (2z3 +1) kongruentno 5 (mod 8)
7 ^ t2 kongruentno -1 ili 1 (mod 8)
Iz ovoga zakljucujem da je 7 ^ t2 - 5 ^ z2 = 4 , odnosno 7 ^ t2 = 4 + 5 ^ z2
Sada to uvrstimo u drugu zagradu koja postaje :
2 * 5 ^z2 + 4 , sto bi trebalo biti dijeljivo s 3 , no to nije moguće s obzirom da je z2 neprano -> sustav nema riješenja.
2. slučaj, 7 ^ t2 + 5 ^ z2 = 2 ^ k, >= 12
Broj koji je veći od 12 i potencija boja dva mora biti dijeljiv s 8 , pa zaključujemo da je t2 neparan.
Kada promatramo drugu zagradu RHS pocetnog izraza , (7 ^ t2 - 5 ^ z2) , znamo da ona mora biti dijeljiva s 3 , pa zakljucujemo z2 paran.
Također kada promatramo zagradu vidimo iz uvjeta z2 paran , t2 neparan da ona nije dijeljiva s 4 , pa mozemo izraz napisati kao :
7 ^ t2 = 5 ^ z2 + 2*3^n , pa to uvrstimo u prvu zagradu i dobijemo :
2 * 5 ^ z2 + 2*3^n = 2^k , a ovdje znamo da je desna strana dijeljiva s 8 , pa ovaj sustav također nema riješenja.
Dakle u konačnici su jedina riješenja : X = 3 , Y = 1 , Z = 2 i T = 2.
1. Promatramo (mod 3) , iz cega zaključujemo :
2^x*3^y kongurentno 0 (mod 3) i 7^t kongurentno 1 (mod 3) -> 5^z kongruento 1 (mod 3) -> z paran
z = 2*z2
2. Promatramo (mod 8)
1. slucaj , x=1 :
2*3^y kongruento 6 ili 2 (mod 8) *
5^(2*z2) kongruento 1 (mod 8) **
7^t kongruento -1 ili 1 (mod 8) ***
Ovaj sustav ima riješenje samo kada je * kongurento 6 , a *** -1 (mod 8) , pa su y i t neparni.
Sada promatramo (mod 5) u sustavu 2 * 3^( 2*y2 + 1 ) + 5 ^ ( 2*z2 ) = 7^( 2*t2 + 1 )
Vidimo da je prvi član kongurentan 1 ili 4 , a RHS 3 ili 2 (mod 5) , pa zaključujemo da ovaj sustav nema riješenja.
2. slučaj , x = 2 :
4*3^y kongruento 4 (mod 8)
5^(2*z2) kongruento 1 (mod 8)
7^t kongruento -1 ili 1 (mod 8)
Očito , ovaj sustav nema riješenja.
3. slučaj , x >= 3
Sada primjećujemo da 7^t mora biti kongruentno 1 mod 8 , pa je t paran -> t = 2*t2
Kada prebacimo 2. član LHS na desnu stranu dobijemo sljedeći izgled jednadžbe :
2^x * 3^y = (7 ^ t2 - 5 ^ z2) (7 ^ t2 + 5 ^ z2)
U ovoj jednažbi primjećujemo da ako je jedna zagrada RHS-a dijeljiva s 3 , druga nije , a ta koja nije mora biti isključivo potencija broja 2, pa mozemo promatramo 2 slučaja :
1. slučaj 7 ^ t2 - 5 ^ z2 = 2 ^ k
1. 1. : t2 = 1 , z2 = 1 :
riješenja ovoga ispadnu x = 3 , y = 1 , z = 2 , t = 2 , donosno
2^3 * 3 + 5^2 = 7^2
1. 2. !(t2 = 1 & z2 = 1)
Kako je 7 ^ t2 + 5 ^ z2 dijeljivo s 3 , zakljucujemo da je z2 neparan , z2 = 2z3 + 1
Gledamo (mod 8) :
5 ^ (2z3 +1) kongruentno 5 (mod 8)
7 ^ t2 kongruentno -1 ili 1 (mod 8)
Iz ovoga zakljucujem da je 7 ^ t2 - 5 ^ z2 = 4 , odnosno 7 ^ t2 = 4 + 5 ^ z2
Sada to uvrstimo u drugu zagradu koja postaje :
2 * 5 ^z2 + 4 , sto bi trebalo biti dijeljivo s 3 , no to nije moguće s obzirom da je z2 neprano -> sustav nema riješenja.
2. slučaj, 7 ^ t2 + 5 ^ z2 = 2 ^ k, >= 12
Broj koji je veći od 12 i potencija boja dva mora biti dijeljiv s 8 , pa zaključujemo da je t2 neparan.
Kada promatramo drugu zagradu RHS pocetnog izraza , (7 ^ t2 - 5 ^ z2) , znamo da ona mora biti dijeljiva s 3 , pa zakljucujemo z2 paran.
Također kada promatramo zagradu vidimo iz uvjeta z2 paran , t2 neparan da ona nije dijeljiva s 4 , pa mozemo izraz napisati kao :
7 ^ t2 = 5 ^ z2 + 2*3^n , pa to uvrstimo u prvu zagradu i dobijemo :
2 * 5 ^ z2 + 2*3^n = 2^k , a ovdje znamo da je desna strana dijeljiva s 8 , pa ovaj sustav također nema riješenja.
Dakle u konačnici su jedina riješenja : X = 3 , Y = 1 , Z = 2 i T = 2.
Komentari:
grga, 28. listopada 2015. 14:21
 Školjka
Školjka 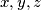 and
and  such that
such that 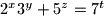
 ? (npr za
? (npr za 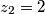 ,
, 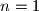 ?)
?)