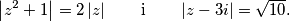Točno
14. travnja 2012. 11:37 (13 godine, 10 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
|z^2+1|=2*|z|
|a^2+2*a*b*i-b^2|=2*|a+b*i| /^2
koristeći formulu |z|^2=a^2+b^2 dobije se:
a^4+b^4+2*a^2*b^2+1-2a^2-6b^2=0
tj.:
(a^2+b^2-2)*(a^2+b^2)+1-4b^2 (1)
______________________________
2. uvjet:
|a+b*i-3*i|=10^0,5 /^2
sređivanjem dobijemo:
a^2+b^2-6b=1
a^2+b^2=1+6b
uvrstimo to u jednadžbu (1)
(6b+1)*(6b-1)+1-4b^2=0
32b^2=0
b^2=0
b=0
vrijedi: a^2+b^2-6b=1 tj.
a^2=1
a=+-1
z1=1 z2=-1
Ako uvrstimo vidjet cemo da vrijedi
|a^2+2*a*b*i-b^2|=2*|a+b*i| /^2
koristeći formulu |z|^2=a^2+b^2 dobije se:
a^4+b^4+2*a^2*b^2+1-2a^2-6b^2=0
tj.:
(a^2+b^2-2)*(a^2+b^2)+1-4b^2 (1)
______________________________
2. uvjet:
|a+b*i-3*i|=10^0,5 /^2
sređivanjem dobijemo:
a^2+b^2-6b=1
a^2+b^2=1+6b
uvrstimo to u jednadžbu (1)
(6b+1)*(6b-1)+1-4b^2=0
32b^2=0
b^2=0
b=0
vrijedi: a^2+b^2-6b=1 tj.
a^2=1
a=+-1
z1=1 z2=-1
Ako uvrstimo vidjet cemo da vrijedi
Ocjene: (1)
Komentari:
Filip_Wee, 14. travnja 2012. 16:47
grga, 14. travnja 2012. 14:15
u 2. redu ti fali +1 lijevo, al osim toga je dobro.
probaj pisat dolar simbole kad pises mat. formule, drugima ce bit puno citljivije, a stvarno se lako koriste. evo pogledaj kak to izgleda, sam cu stavit dolar na pocetak i kraj i svake jednadbe:
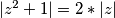
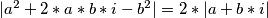 /^2
/^2
koristeći formulu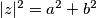 dobije se:
dobije se:
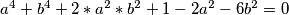
tj.:
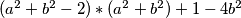 (1)
(1)
______________________________
2. uvjet:
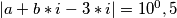 /^2
/^2
sređivanjem dobijemo:
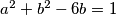
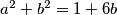
uvrstimo to u jednadžbu (1)
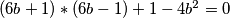
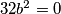
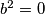
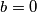
vrijedi: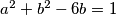 tj.
tj.
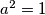
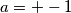
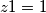
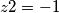
Ako uvrstimo vidjet cemo da vrijedi
sad, naravno, ovjde je bolje ne pisat " " jer ruzno izgleda, i ovo
" jer ruzno izgleda, i ovo 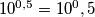 je ruzno ispalo. naravno, uvjek mozes koristit i
je ruzno ispalo. naravno, uvjek mozes koristit i 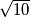 . takoder, za plusminus imas
. takoder, za plusminus imas 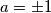 , te za indexe
, te za indexe 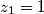 ,
, 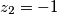 .
.
nije ovo sve nuzno al ono, ak stignes, probaj ovak uredit. a ionako ce ti latex kad tad trebat. cini mi se da je najlakse naucit tak da quotas ono kaj su drugi pisali pa vidis kak se to radi.
probaj pisat dolar simbole kad pises mat. formule, drugima ce bit puno citljivije, a stvarno se lako koriste. evo pogledaj kak to izgleda, sam cu stavit dolar na pocetak i kraj i svake jednadbe:
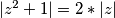
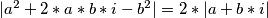 /^2
/^2koristeći formulu
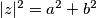 dobije se:
dobije se: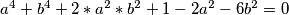
tj.:
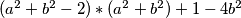 (1)
(1)______________________________
2. uvjet:
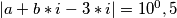 /^2
/^2sređivanjem dobijemo:
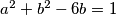
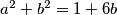
uvrstimo to u jednadžbu (1)
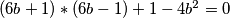
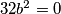
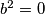
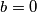
vrijedi:
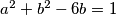 tj.
tj.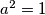
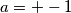
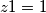
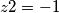
Ako uvrstimo vidjet cemo da vrijedi
sad, naravno, ovjde je bolje ne pisat "
 " jer ruzno izgleda, i ovo
" jer ruzno izgleda, i ovo 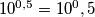 je ruzno ispalo. naravno, uvjek mozes koristit i
je ruzno ispalo. naravno, uvjek mozes koristit i 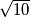 . takoder, za plusminus imas
. takoder, za plusminus imas 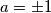 , te za indexe
, te za indexe 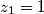 ,
, 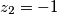 .
. nije ovo sve nuzno al ono, ak stignes, probaj ovak uredit. a ionako ce ti latex kad tad trebat. cini mi se da je najlakse naucit tak da quotas ono kaj su drugi pisali pa vidis kak se to radi.
Zadnja promjena: grga, 14. travnja 2012. 14:34
 Školjka
Školjka  takve da vrijedi
takve da vrijedi