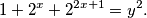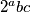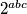Točno
14. travnja 2012. 16:26 (13 godine, 10 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
ako je x<-1 onda 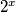 i
i 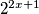 nisu cjelobrojni. sada dokažimo da i njihov zbroj nije cjelobrojan.
nisu cjelobrojni. sada dokažimo da i njihov zbroj nije cjelobrojan.
Kako bi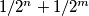 ,
, 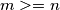 bio cjelobrojan, oni moraju biti isti i moraju biti
bio cjelobrojan, oni moraju biti isti i moraju biti 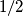
dokaz: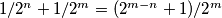 što je cjelobrojno kada je
što je cjelobrojno kada je 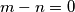 i
i 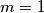 ---->
---->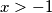
izlučimo 2^x te oduzmemo 1 od cijele jednadžbe i dobimo:
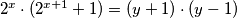
kako su y-1 i y+1 udaljeni za 2, jedan od njih je djeljiv s 2 i ne sa 4 tako da:
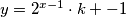
Gdje je k neparan
uvrstimo to u jednadžbu:
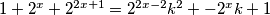
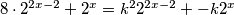
1. +
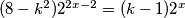
k<3
a) k=2 --->k mora biti neparan
b) k=1
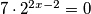
x ne postoji
2. -
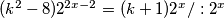 }
}
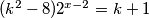
x>=0 (jer ako je manji od 0 onda y nije cijeli broj)
x=0 onda je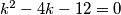 rješenja su -2,6 tj. y= -2,0,2,4 a rješenja su 2,-2 jer moraju biti suprotnog predznaka. kako je y rješenje mora biti rješenje i -y. a 0 nije rješenje jer lijeva strana nije 0.
rješenja su -2,6 tj. y= -2,0,2,4 a rješenja su 2,-2 jer moraju biti suprotnog predznaka. kako je y rješenje mora biti rješenje i -y. a 0 nije rješenje jer lijeva strana nije 0.
x=0 ---->y=+-2 tj; (x,y)=(0,2),(0,-2)
x=1
y nije cjelobrojan
x=2
y nije cjelobrojan
x=3
y nije cjelobrojan
x=4
y=+-23
(x,y)=(4,23),(4,-23)
ako je x>=5
k nesmije biti veći od 4 (kada je veći od 4, x mora biti manji od 5 ni manji jednak -3 jer je inače desna strana manja od lijeve. Također, k je neparan
ostaje nam:
k=-1 ->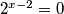 nema rješenja
nema rješenja
k=1 ->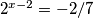 nema rješenja
nema rješenja
k=3 -> x=4, y=+-23
I to su sva rješenja:
(x,y)=(0,2),(0,-2),(4,23),(4,-23)
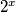 i
i 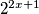 nisu cjelobrojni. sada dokažimo da i njihov zbroj nije cjelobrojan.
nisu cjelobrojni. sada dokažimo da i njihov zbroj nije cjelobrojan.Kako bi
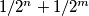 ,
, 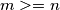 bio cjelobrojan, oni moraju biti isti i moraju biti
bio cjelobrojan, oni moraju biti isti i moraju biti 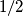
dokaz:
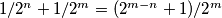 što je cjelobrojno kada je
što je cjelobrojno kada je 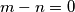 i
i 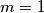 ---->
---->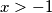
izlučimo 2^x te oduzmemo 1 od cijele jednadžbe i dobimo:
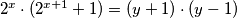
kako su y-1 i y+1 udaljeni za 2, jedan od njih je djeljiv s 2 i ne sa 4 tako da:
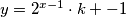
Gdje je k neparan
uvrstimo to u jednadžbu:
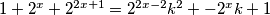
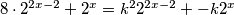
1. +
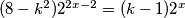
k<3
a) k=2 --->k mora biti neparan
b) k=1
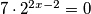
x ne postoji
2. -
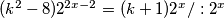 }
}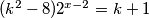
x>=0 (jer ako je manji od 0 onda y nije cijeli broj)
x=0 onda je
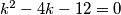 rješenja su -2,6 tj. y= -2,0,2,4 a rješenja su 2,-2 jer moraju biti suprotnog predznaka. kako je y rješenje mora biti rješenje i -y. a 0 nije rješenje jer lijeva strana nije 0.
rješenja su -2,6 tj. y= -2,0,2,4 a rješenja su 2,-2 jer moraju biti suprotnog predznaka. kako je y rješenje mora biti rješenje i -y. a 0 nije rješenje jer lijeva strana nije 0.x=0 ---->y=+-2 tj; (x,y)=(0,2),(0,-2)
x=1
y nije cjelobrojan
x=2
y nije cjelobrojan
x=3
y nije cjelobrojan
x=4
y=+-23
(x,y)=(4,23),(4,-23)
ako je x>=5
k nesmije biti veći od 4 (kada je veći od 4, x mora biti manji od 5 ni manji jednak -3 jer je inače desna strana manja od lijeve. Također, k je neparan
ostaje nam:
k=-1 ->
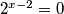 nema rješenja
nema rješenjak=1 ->
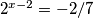 nema rješenja
nema rješenjak=3 -> x=4, y=+-23
I to su sva rješenja:
(x,y)=(0,2),(0,-2),(4,23),(4,-23)
Ocjene: (1)
Komentari:
grga, 16. travnja 2012. 19:20
ok. super. imas pravo, neznam zasto sam mislio da bi tamo trebao biti minus.
sta se tice ovoga
k nesmije biti veći od 4 (kada je veći od 4, x mora biti manji od 5 ni manji jednak -3 jer je inače desna strana manja od lijeve. Također, k je neparan
je da je ocito, al evo malo formalnije, za slucaj da nekom nije jasno
pretpostavimo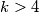
tada je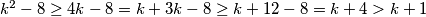
pa onda ako jos imamo desno pomnozeno s onim nekom potencijom od , jasno je da ce desna biti jos veca.
, jasno je da ce desna biti jos veca.
sta se tice ovoga
k nesmije biti veći od 4 (kada je veći od 4, x mora biti manji od 5 ni manji jednak -3 jer je inače desna strana manja od lijeve. Također, k je neparan
je da je ocito, al evo malo formalnije, za slucaj da nekom nije jasno
pretpostavimo
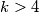
tada je
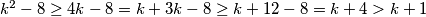
pa onda ako jos imamo desno pomnozeno s onim nekom potencijom od
 , jasno je da ce desna biti jos veca.
, jasno je da ce desna biti jos veca. Filip_Wee, 16. travnja 2012. 16:52
ikicic, 16. travnja 2012. 16:48
Filip_Wee, 16. travnja 2012. 00:52
Slucaj 2.- mi je ok mislim jer imam 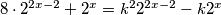
iz toga dodje ovaj izraz sa k+1, prebacim k lijevo, a k^2 desno
I probao sam za x je 0 1 2 3 4
 je cjelobrojan po uvjetu zadataka.
je cjelobrojan po uvjetu zadataka.
ok, sad mi se cini vise manje dobro, ali idalje ne bi li ti trebalo biti kod ovog slucaja "2. - "
pa onda s desne strane u zagradi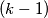 .. ? onda dobijes nesto drugaciji racun, al u principu je ideja dobra.
.. ? onda dobijes nesto drugaciji racun, al u principu je ideja dobra.
jos jedna stvar.. ti iz jednadbe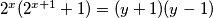 i cinjenice da je
i cinjenice da je 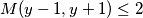 zakljucujes oblik broja
zakljucujes oblik broja  , na temelju djeljivosti s
, na temelju djeljivosti s  . da sam ja na natjecanju, eventualno bih bio malo pazljiviji, pa bi za
. da sam ja na natjecanju, eventualno bih bio malo pazljiviji, pa bi za 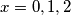 prvojerio rucno ( jer te ne kosta previse vremena ), a onda za
prvojerio rucno ( jer te ne kosta previse vremena ), a onda za 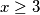 si siguran da ti je zakljucak o izgledu broja
si siguran da ti je zakljucak o izgledu broja  valjan. tj neznam, mozda si ti siguran i za ove male
valjan. tj neznam, mozda si ti siguran i za ove male  , al meni nije to bas tako ocito.
, al meni nije to bas tako ocito.
par stvari glede latexa: razlomak ljepse izgleda ovako , a plusminus ovako
, a plusminus ovako 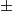
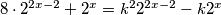
iz toga dodje ovaj izraz sa k+1, prebacim k lijevo, a k^2 desno
I probao sam za x je 0 1 2 3 4
 je cjelobrojan po uvjetu zadataka.
je cjelobrojan po uvjetu zadataka.ok, sad mi se cini vise manje dobro, ali idalje ne bi li ti trebalo biti kod ovog slucaja "2. - "
pa onda s desne strane u zagradi
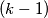 .. ? onda dobijes nesto drugaciji racun, al u principu je ideja dobra.
.. ? onda dobijes nesto drugaciji racun, al u principu je ideja dobra.jos jedna stvar.. ti iz jednadbe
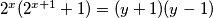 i cinjenice da je
i cinjenice da je 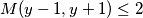 zakljucujes oblik broja
zakljucujes oblik broja  , na temelju djeljivosti s
, na temelju djeljivosti s  . da sam ja na natjecanju, eventualno bih bio malo pazljiviji, pa bi za
. da sam ja na natjecanju, eventualno bih bio malo pazljiviji, pa bi za 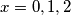 prvojerio rucno ( jer te ne kosta previse vremena ), a onda za
prvojerio rucno ( jer te ne kosta previse vremena ), a onda za 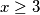 si siguran da ti je zakljucak o izgledu broja
si siguran da ti je zakljucak o izgledu broja  valjan. tj neznam, mozda si ti siguran i za ove male
valjan. tj neznam, mozda si ti siguran i za ove male  , al meni nije to bas tako ocito.
, al meni nije to bas tako ocito.par stvari glede latexa: razlomak ljepse izgleda ovako
 , a plusminus ovako
, a plusminus ovako 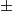
grga, 15. travnja 2012. 23:56
 je cjelobrojan po uvjetu zadataka.
je cjelobrojan po uvjetu zadataka.ok, sad mi se cini vise manje dobro, ali idalje ne bi li ti trebalo biti kod ovog slucaja "2. - "
pa onda s desne strane u zagradi
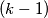 .. ? onda dobijes nesto drugaciji racun, al u principu je ideja dobra.
.. ? onda dobijes nesto drugaciji racun, al u principu je ideja dobra.jos jedna stvar.. ti iz jednadbe
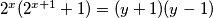 i cinjenice da je
i cinjenice da je 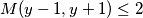 zakljucujes oblik broja
zakljucujes oblik broja  , na temelju djeljivosti s
, na temelju djeljivosti s  . da sam ja na natjecanju, eventualno bih bio malo pazljiviji, pa bi za
. da sam ja na natjecanju, eventualno bih bio malo pazljiviji, pa bi za 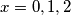 prvojerio rucno ( jer te ne kosta previse vremena ), a onda za
prvojerio rucno ( jer te ne kosta previse vremena ), a onda za 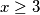 si siguran da ti je zakljucak o izgledu broja
si siguran da ti je zakljucak o izgledu broja  valjan. tj neznam, mozda si ti siguran i za ove male
valjan. tj neznam, mozda si ti siguran i za ove male  , al meni nije to bas tako ocito.
, al meni nije to bas tako ocito.par stvari glede latexa: razlomak ljepse izgleda ovako
 , a plusminus ovako
, a plusminus ovako 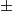
ikicic, 15. travnja 2012. 22:50
Filip_Wee, 15. travnja 2012. 21:49
grga, 15. travnja 2012. 15:18
integers su cijeli brojevi, ne nuzno prirodni, zar ne? cini mi se da ti onda onaj zakljucak u drugom - trecem redu da je 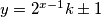 bas ne stoji.. ono, s lijeve strane mozes imat nekakve razlomke i neka cuda. mozda i stoji, al u najmanju ruku moras to malo bolje objasnit.
bas ne stoji.. ono, s lijeve strane mozes imat nekakve razlomke i neka cuda. mozda i stoji, al u najmanju ruku moras to malo bolje objasnit.
sta i ne bi trebalo biti tamo ispod "1. +", pa onda s desne strane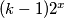 .. isto za ovo ispod "2. -"
.. isto za ovo ispod "2. -"
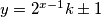 bas ne stoji.. ono, s lijeve strane mozes imat nekakve razlomke i neka cuda. mozda i stoji, al u najmanju ruku moras to malo bolje objasnit.
bas ne stoji.. ono, s lijeve strane mozes imat nekakve razlomke i neka cuda. mozda i stoji, al u najmanju ruku moras to malo bolje objasnit.sta i ne bi trebalo biti tamo ispod "1. +", pa onda s desne strane
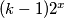 .. isto za ovo ispod "2. -"
.. isto za ovo ispod "2. -" Filip_Wee, 14. travnja 2012. 19:58
Filip_Wee, 14. travnja 2012. 19:41
ikicic, 14. travnja 2012. 19:27
Filip_Wee, 14. travnja 2012. 19:00
Filip_Wee, 14. travnja 2012. 18:40
kokan, 14. travnja 2012. 18:32
naredbe u latexu se pisu s \ ispred, a ne /. :)
mozda je nepotrebno pisati tutorial kad tu ima sve: http://en.wikibooks.org/wiki/LaTeX, a pod http://en.wikibooks.org/wiki/LaTeX/Mathematics pogotovo. a najbolje se uci kad se vidi kako drugi pisu.
ako pod u matematicki dio treba ubaciti tekst, koristiti \text{.....}.
i za iff recimo \Longleftrightarrow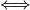
i naravno, procitati ono na dnu http://skoljka.no-ip.org/help/ za pocetak.
nije lose uvijek pisati zagrade automatske velicine: \left(, \right), \left[, \right], \left\{, \right\}. detalj po detalj i nauci se. :)
za pomoc uvijek mozes pitati na https://www.facebook.com/pages/TeXLaTeX-savjeti/261129223970236
mozda je nepotrebno pisati tutorial kad tu ima sve: http://en.wikibooks.org/wiki/LaTeX, a pod http://en.wikibooks.org/wiki/LaTeX/Mathematics pogotovo. a najbolje se uci kad se vidi kako drugi pisu.
ako pod u matematicki dio treba ubaciti tekst, koristiti \text{.....}.
i za iff recimo \Longleftrightarrow
i naravno, procitati ono na dnu http://skoljka.no-ip.org/help/ za pocetak.
nije lose uvijek pisati zagrade automatske velicine: \left(, \right), \left[, \right], \left\{, \right\}. detalj po detalj i nauci se. :)
za pomoc uvijek mozes pitati na https://www.facebook.com/pages/TeXLaTeX-savjeti/261129223970236
Ok evo ispravit cu :D tutorial bi bio super hehe
Zadnja promjena: kokan, 14. travnja 2012. 18:41
Filip_Wee, 14. travnja 2012. 18:16
kokan, 14. travnja 2012. 17:42
ikicic, 14. travnja 2012. 17:20
Filip_Wee, 14. travnja 2012. 16:27
 Školjka
Školjka 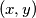 of integers such that
of integers such that