Točno
14. travnja 2012. 20:23 (13 godine, 10 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
1) a+1=b^2-4ac
2) a+2=c/a
3) a+3=-b/a
iz 2) se vidi da a|c
iz 3) se vidi da a|b
1)
a+1=b^2-4ac
a+4ac=b^2-1
a(1+4c)=(b-1)(b+1)
što znači da a djeli ili b-1, ili b+1, te iz 3) se vidi da djeli b, što znači da a djeli 2 uzastopna broja
to je moguće samo ako je a=+-1
provjeravanjem se vidi da je jedino rješenje a=-1
2) a+2=c/a
3) a+3=-b/a
iz 2) se vidi da a|c
iz 3) se vidi da a|b
1)
a+1=b^2-4ac
a+4ac=b^2-1
a(1+4c)=(b-1)(b+1)
što znači da a djeli ili b-1, ili b+1, te iz 3) se vidi da djeli b, što znači da a djeli 2 uzastopna broja
to je moguće samo ako je a=+-1
provjeravanjem se vidi da je jedino rješenje a=-1
 Školjka
Školjka 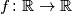 kvadratna funkcija
kvadratna funkcija 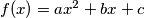 . Označimo sa
. Označimo sa  diskriminantu, sa
diskriminantu, sa  umnožak, a sa
umnožak, a sa  zbroj njezinih nultočaka. Pokažite da postoji samo jedna funkcija
zbroj njezinih nultočaka. Pokažite da postoji samo jedna funkcija  za koju su
za koju su  ,
,