Točno
11. travnja 2015. 20:34 (10 godine, 10 mjeseci)
Niz
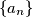
je zadan na ovaj način:
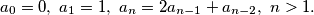
Dokažite da
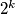
dijeli

ako i samo ako
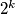
dijeli

.
%V0
Niz $\{ a_n \} $ je zadan na ovaj način:
$$ a_0=0, \ a_1=1, \ a_n=2a_{n-1}+a_{n-2}, \ n>1.$$
Dokažite da $2^k$ dijeli $a_n$ ako i samo ako $2^k$ dijeli $n$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
%V0
Indukcijom dokazemo relaciju:
$ a_n = a_{n-k} \cdot a_{k+1} + a_{n-k-1} \cdot a_{k} $
Uvrstimo $n = 2k$
$ a_{2k} = a_{k} \cdot a_{k+1} + a_{k-1} \cdot a_{k} $
$ a_{2k} = a_{k} (a_{k+1} + a_{k-1}) $
$ a_{2k} = 2a_{k} (a_{k} + a_{k-1}) $
No $(a_{k} + a_{k-1})$ je ocito neparan dakle:
$v_2(a_{2k}) = 1 + v_2(a_k)$
Te uz $v_2(a_{2k+1}) = 0$ zakljucujemo $v_2(a_k) = v_2(k)$
| 26. travnja 2015. 19:34 | ikicic | Točno |