Točno
11. travnja 2015. 21:10 (10 godine, 11 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Primjetimo da ne postoji  takav da
takav da 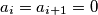 (jer to implicira
(jer to implicira 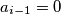 , dakle
, dakle 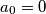 ).
).
Ako uparimo svaku nulu sa nenula brojem na lijevo, primjetimo da svaki broj se nalazi u najvise jednom paru, te broj parova je jednak broju nuli, dakle broj nula je najvise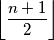 .
.
Dakle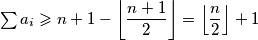
Nadalje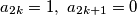 je valjana konstrukcija za koju postizemo sumu
je valjana konstrukcija za koju postizemo sumu 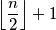 , pa je ekvivalentno dokazati (i evaluirati jednakost za):
, pa je ekvivalentno dokazati (i evaluirati jednakost za):
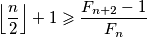
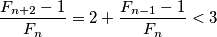 dakle vrijedi stroga nejednakost za
dakle vrijedi stroga nejednakost za 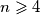
Jednakost vrijedi samo za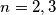
 takav da
takav da 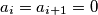 (jer to implicira
(jer to implicira 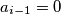 , dakle
, dakle 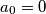 ).
).Ako uparimo svaku nulu sa nenula brojem na lijevo, primjetimo da svaki broj se nalazi u najvise jednom paru, te broj parova je jednak broju nuli, dakle broj nula je najvise
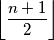 .
.Dakle
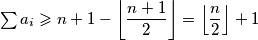
Nadalje
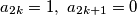 je valjana konstrukcija za koju postizemo sumu
je valjana konstrukcija za koju postizemo sumu 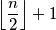 , pa je ekvivalentno dokazati (i evaluirati jednakost za):
, pa je ekvivalentno dokazati (i evaluirati jednakost za):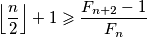
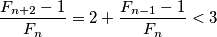 dakle vrijedi stroga nejednakost za
dakle vrijedi stroga nejednakost za 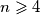
Jednakost vrijedi samo za
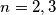
 Školjka
Školjka 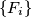 ,
, 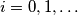 niz brojeva definiran na sljedeći način:
niz brojeva definiran na sljedeći način: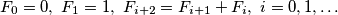
 neka su
neka su 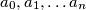 nenegativni brojevi koji zadovoljavaju uvjet
nenegativni brojevi koji zadovoljavaju uvjet 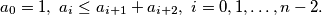
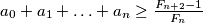 . Da li se postiže jednakost?
. Da li se postiže jednakost? 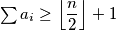 , dovoljno je pokazati da je
, dovoljno je pokazati da je 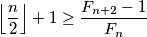 , pa će automatski biti zadovoljena tvrdnja zadatka.
, pa će automatski biti zadovoljena tvrdnja zadatka.