Školjka

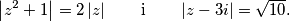
%V0 S obzirom da je $z^2 = zz$, slijedi $|z^2| = |z||z| = |z|^2$, pa imamo: $||z|^2 + 1| = 2|z|$ $|z|^2 + 1 = 2|z|$ $|z|^2 - 2|z| + 1 = 0$ $(|z| - 1)^2 = 0 /^{\sqrt{}}$ $|z| - 1 = 0$ $|z| = 1$ $z \in \mathbb{C} \Rightarrow |z|^2 = \Re(z)^2 + \Im(z)^2$ $|z - 3i|^2 = 10$ $\Re(z-3i)^2 + \Im(z-3i)^2 = 10$ $(\Re(z) + \Re(-3i))^2 + (\Im(z) + \Im(-3i))^2 = 10$ $\Re(z)^2 + (\Im(z) - 3)^2 = 10$ $\Re(z)^2 + \Im(z)^2 - 6\Im(z) + 9 = 10$ $|z| - 6\Im(z) = 1$ $1 - 6\Im(z) = 1$ $-6\Im(z) = 0$ $\Im(z) = 0$ A iz $|z| = 1, \Im(z) = 0$ slijedi $\Re(z)^2 = 1 /^{\sqrt{}}$ $\Re(z) = \pm 1$ a s obzirom da je $z = \Re(z) + i\Im(z)$ $z_{1,2} = \pm 1$