50%
15. travnja 2012. 18:54 (13 godine, 11 mjeseci)
Neka je skup prirodnih brojeva podijeljen u intervale na sljedeći način:
U prvom intervalu je broj 1, u drugom brojevi 2 i 3, u trećem 4, 5 i 6 i u svakom idućem jedan broj više nego u prethodnom (brojevi u intervalima su uzastopni).
Neka je udio prostih brojeva u
udio prostih brojeva u  -tom intervalu.
-tom intervalu.
a) Dokaži ili opovrgni: Postoji beskonačno brojeva za koje je
za koje je 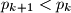 .
.
b) Dokaži ili opovrgni: Postoji beskonačno brojeva za koje je
za koje je 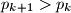 .
.
U prvom intervalu je broj 1, u drugom brojevi 2 i 3, u trećem 4, 5 i 6 i u svakom idućem jedan broj više nego u prethodnom (brojevi u intervalima su uzastopni).
Neka je
 udio prostih brojeva u
udio prostih brojeva u  -tom intervalu.
-tom intervalu.a) Dokaži ili opovrgni: Postoji beskonačno brojeva
 za koje je
za koje je 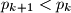 .
.b) Dokaži ili opovrgni: Postoji beskonačno brojeva
 za koje je
za koje je 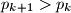 .
. Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
a)
Pretpostavimo da postoji samo konačno -ova t. d. vrijedi
-ova t. d. vrijedi 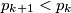 . To znači da od nekog
. To znači da od nekog 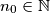 nadalje udjeli rastu. Očito, ako raste udio, mora rasti i broj prostih (
nadalje udjeli rastu. Očito, ako raste udio, mora rasti i broj prostih (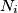 ) po intervalu. Iz toga se vidi da je
) po intervalu. Iz toga se vidi da je 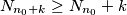 . Posebno,
. Posebno, 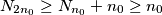 . Iz toga imamo
. Iz toga imamo 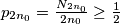 , što je nemoguće (čak i kad bi svaki neparni bio prost:) )
, što je nemoguće (čak i kad bi svaki neparni bio prost:) )
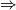 Postoji ih beskonačno.
Postoji ih beskonačno.
b)
Opet, pretpostavimo da postoji samo konačno takvih -ova. To znači da od nekog
-ova. To znači da od nekog 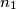 nadalje udio pada. Lako se vidi da tada broj prostih stagnira ili pada. Dobivamo da za
nadalje udio pada. Lako se vidi da tada broj prostih stagnira ili pada. Dobivamo da za 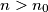 vrijedi
vrijedi 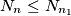 , tj. broj prostih u intervalima je odozgo ograničen. To je također nemoguće (što se vidi iz, npr, "Bertrandovog postulata").
, tj. broj prostih u intervalima je odozgo ograničen. To je također nemoguće (što se vidi iz, npr, "Bertrandovog postulata").
Pretpostavimo da postoji samo konačno
 -ova t. d. vrijedi
-ova t. d. vrijedi 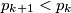 . To znači da od nekog
. To znači da od nekog 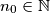 nadalje udjeli rastu. Očito, ako raste udio, mora rasti i broj prostih (
nadalje udjeli rastu. Očito, ako raste udio, mora rasti i broj prostih (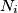 ) po intervalu. Iz toga se vidi da je
) po intervalu. Iz toga se vidi da je 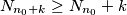 . Posebno,
. Posebno, 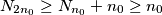 . Iz toga imamo
. Iz toga imamo 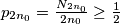 , što je nemoguće (čak i kad bi svaki neparni bio prost:) )
, što je nemoguće (čak i kad bi svaki neparni bio prost:) )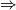 Postoji ih beskonačno.
Postoji ih beskonačno.b)
Opet, pretpostavimo da postoji samo konačno takvih
 -ova. To znači da od nekog
-ova. To znači da od nekog 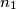 nadalje udio pada. Lako se vidi da tada broj prostih stagnira ili pada. Dobivamo da za
nadalje udio pada. Lako se vidi da tada broj prostih stagnira ili pada. Dobivamo da za 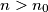 vrijedi
vrijedi 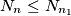 , tj. broj prostih u intervalima je odozgo ograničen. To je također nemoguće (što se vidi iz, npr, "Bertrandovog postulata").
, tj. broj prostih u intervalima je odozgo ograničen. To je također nemoguće (što se vidi iz, npr, "Bertrandovog postulata"). Ocjene: (4)
Komentari:
pbakic, 19. travnja 2012. 15:02
Uf, istina, izgledalo mi je preočito pa sam malo požurio s rješenjem :)
Vidio sam tvoje, najs je
Vidio sam tvoje, najs je
moze se izbjeci bertrandov postulat koji nije elementaran, ali nisam siguran da to slijedi iz bertrandovog postulata (izmedu n i 2n postoji prost broj) jer cak i ne postoji interval u kojemu su i n i 2n...
dcevid, 19. travnja 2012. 13:23
Filip_Wee, 16. travnja 2012. 18:05
 Školjka
Školjka