Točno
10. siječnja 2016. 19:47 (10 godine)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
domisljat naziv :)
opcenito napisimo prirodni u rastavu na proste faktore:
u rastavu na proste faktore: 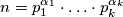 .
.
tada je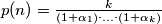 .
.
(a) jasno da je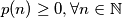 , i da se
, i da se  postize ako i samo ako je
postize ako i samo ako je 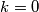 , tj
, tj 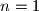 .
.
takoder, iako zadatak to eksplicitno ne trazi, zanimljivo je vidjeti da za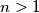 prostotak moze doci proizvoljno blizu
prostotak moze doci proizvoljno blizu  , ali jasno ne moze bas biti
, ali jasno ne moze bas biti  . npr za niz
. npr za niz 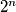 , odgovarajuci niz prostotaka je
, odgovarajuci niz prostotaka je 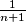 , sto moze biti po volji malo, ali nikada bas
, sto moze biti po volji malo, ali nikada bas  .
.
(b) za fixni , prostotak se ocito maximizira za
, prostotak se ocito maximizira za 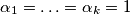 . trazimo dakle maksimum od
. trazimo dakle maksimum od 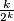 . za
. za 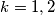 , ova funkcija ima vrijednost
, ova funkcija ima vrijednost  . za
. za 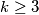 je funkcija strogo padajuca sto nije tesko vidjeti deriviranjem ili npr indukcijom. zato najveci prostotak imaju oni prirodni brojevi koji su prosti ili umnozak dva razlicita prosta broja, i njihov prostotak iznosi
je funkcija strogo padajuca sto nije tesko vidjeti deriviranjem ili npr indukcijom. zato najveci prostotak imaju oni prirodni brojevi koji su prosti ili umnozak dva razlicita prosta broja, i njihov prostotak iznosi  .
.
opcenito napisimo prirodni
 u rastavu na proste faktore:
u rastavu na proste faktore: 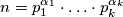 .
.tada je
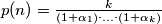 .
.(a) jasno da je
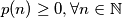 , i da se
, i da se  postize ako i samo ako je
postize ako i samo ako je 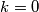 , tj
, tj 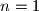 .
.takoder, iako zadatak to eksplicitno ne trazi, zanimljivo je vidjeti da za
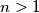 prostotak moze doci proizvoljno blizu
prostotak moze doci proizvoljno blizu  , ali jasno ne moze bas biti
, ali jasno ne moze bas biti  . npr za niz
. npr za niz 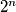 , odgovarajuci niz prostotaka je
, odgovarajuci niz prostotaka je 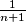 , sto moze biti po volji malo, ali nikada bas
, sto moze biti po volji malo, ali nikada bas  .
.(b) za fixni
 , prostotak se ocito maximizira za
, prostotak se ocito maximizira za 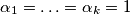 . trazimo dakle maksimum od
. trazimo dakle maksimum od 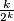 . za
. za 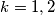 , ova funkcija ima vrijednost
, ova funkcija ima vrijednost  . za
. za 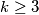 je funkcija strogo padajuca sto nije tesko vidjeti deriviranjem ili npr indukcijom. zato najveci prostotak imaju oni prirodni brojevi koji su prosti ili umnozak dva razlicita prosta broja, i njihov prostotak iznosi
je funkcija strogo padajuca sto nije tesko vidjeti deriviranjem ili npr indukcijom. zato najveci prostotak imaju oni prirodni brojevi koji su prosti ili umnozak dva razlicita prosta broja, i njihov prostotak iznosi  .
.  Školjka
Školjka 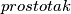 nekog prirodnog broja kao omjer broja njegovih prostih djelitelja i njegovog ukupnog broja djelitelja. (
nekog prirodnog broja kao omjer broja njegovih prostih djelitelja i njegovog ukupnog broja djelitelja. (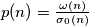 )
) s najmanjim
s najmanjim 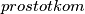
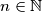 s najvećim
s najvećim