Točno
17. siječnja 2016. 19:01 (8 godine, 10 mjeseci)
Neka su
,
,
pozitivni relani brojevi takvi da je
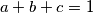
. Dokažite da vrijedi nejednakost
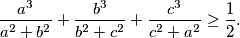
%V0
Neka su $a$, $b$, $c$ pozitivni relani brojevi takvi da je $a + b + c = 1$. Dokažite da vrijedi nejednakost
$$\dfrac{a^3}{a^2 + b^2} + \dfrac{b^3}{b^2 + c^2} + \dfrac{c^3}{c^2 + a^2} \geq \dfrac{1}{2}\text{.}$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
a^3/(a^2+b^2) = a- ab^2/(a^2 + b^2) = a - b/2 ( 2ab/(a^2 + b^2)) , a jer je a^2 + b^2 >= 2ab
a - b/2 ( 2ab/(a^2 + b^2))>= a-b/2 * 1= a-b/2
Tada je
a^3/(a^2+b^2) + b^3/(b^2+c^2) + c^3/(c^2+a^2)>= a - b/2 + b- c/2 + c - a/2 = 1/2( a + b + c) * 1/2
%V0
a^3/(a^2+b^2) = a- ab^2/(a^2 + b^2) = a - b/2 ( 2ab/(a^2 + b^2)) , a jer je a^2 + b^2 >= 2ab
a - b/2 ( 2ab/(a^2 + b^2))>= a-b/2 * 1= a-b/2
Tada je
a^3/(a^2+b^2) + b^3/(b^2+c^2) + c^3/(c^2+a^2)>= a - b/2 + b- c/2 + c - a/2 = 1/2( a + b + c) * 1/2
| 17. siječnja 2016. 22:25 | ikicic | Točno |
Školjka