Točno
23. siječnja 2016. 10:30 (10 godine, 1 mjesec)
Dva igrača,  i
i  igraju sljedeću igru:
igraju sljedeću igru:  i
i  zapisuju naizmjenično po jednu znamenku sve dok ne napišu šesteroznamenkasti broj, pri čemu se niti jedna znamenka ne smije ponoviti. Prva znamenka mora biti različita od
zapisuju naizmjenično po jednu znamenku sve dok ne napišu šesteroznamenkasti broj, pri čemu se niti jedna znamenka ne smije ponoviti. Prva znamenka mora biti različita od  . Igrač
. Igrač  igra prvi, a znamenke se pišu redom slijeva nadesno. Igrač
igra prvi, a znamenke se pišu redom slijeva nadesno. Igrač  pobjeđuje ako je napisani šesteroznamenkasti broj djeljiv s
pobjeđuje ako je napisani šesteroznamenkasti broj djeljiv s  ,
,  ili
ili  , a u suprotnom pobjeđuje igrač
, a u suprotnom pobjeđuje igrač  . Dokaži da igrač
. Dokaži da igrač  ima strategiju za pobjedu, tj. može pobijediti neovisno o igri igrača
ima strategiju za pobjedu, tj. može pobijediti neovisno o igri igrača  .
.
 i
i  igraju sljedeću igru:
igraju sljedeću igru:  i
i  zapisuju naizmjenično po jednu znamenku sve dok ne napišu šesteroznamenkasti broj, pri čemu se niti jedna znamenka ne smije ponoviti. Prva znamenka mora biti različita od
zapisuju naizmjenično po jednu znamenku sve dok ne napišu šesteroznamenkasti broj, pri čemu se niti jedna znamenka ne smije ponoviti. Prva znamenka mora biti različita od  . Igrač
. Igrač  igra prvi, a znamenke se pišu redom slijeva nadesno. Igrač
igra prvi, a znamenke se pišu redom slijeva nadesno. Igrač  pobjeđuje ako je napisani šesteroznamenkasti broj djeljiv s
pobjeđuje ako je napisani šesteroznamenkasti broj djeljiv s  ,
,  ili
ili  , a u suprotnom pobjeđuje igrač
, a u suprotnom pobjeđuje igrač  . Dokaži da igrač
. Dokaži da igrač  ima strategiju za pobjedu, tj. može pobijediti neovisno o igri igrača
ima strategiju za pobjedu, tj. može pobijediti neovisno o igri igrača  .
. Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Napomena: pod kongruencijom uvijek se misli 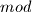
 .
.
Potezi su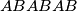 . Primijetimo da ako je zadnja znamenka iz
. Primijetimo da ako je zadnja znamenka iz 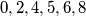 igrač
igrač  gubi. Ako je ta znamenka iz
gubi. Ako je ta znamenka iz 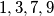 gubitak nije nužan. Zato
gubitak nije nužan. Zato  upisuje jednu od tih znamenaka na kraju, a nijednu prije, jer
upisuje jednu od tih znamenaka na kraju, a nijednu prije, jer  ih treba nastojati ograničiti. Ako su sve znamenke
ih treba nastojati ograničiti. Ako su sve znamenke 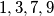 izgubljene na kraju
izgubljene na kraju  nužno gubi.
nužno gubi.
Zato sada trebamo gledati djeljivost sa .
. 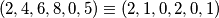 i
i 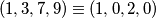 . Imamo nulu viška i to među
. Imamo nulu viška i to među 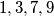 .
.
Strategija igrača je onda riješiti se brojeva
je onda riješiti se brojeva 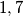 za igrača
za igrača  tako da on na kraju mora napisati
tako da on na kraju mora napisati 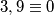 i da da je broj
i da da je broj 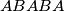 djeljiv s
djeljiv s  .
.
To ostvaruje ovako: U prvom i trećem potezu upisuje i
i  (poredak je nebitan). Zatim u petom potezu upisuje neku znamenku tako da je broj
(poredak je nebitan). Zatim u petom potezu upisuje neku znamenku tako da je broj 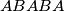 djeljiv s 3.
djeljiv s 3.
Zadnja nada igrača je ograničiti ostatke igraču
je ograničiti ostatke igraču  . To mu ne uspjeva. Ostatak ako zanemarimo poteze igrača
. To mu ne uspjeva. Ostatak ako zanemarimo poteze igrača  je
je  . S dvama dvojkama ostatak je
. S dvama dvojkama ostatak je  pa
pa  samo igra jednu od
samo igra jednu od  . S dvama jedinicima je
. S dvama jedinicima je  i
i  igra dvojku. S dvama nulama
igra dvojku. S dvama nulama  igra jedinicu. Ako
igra jedinicu. Ako  ne igra na taj način
ne igra na taj način  jednostavno ima sve ostatke na raspolaganju. Dakle,
jednostavno ima sve ostatke na raspolaganju. Dakle,  pobjeđuje.
pobjeđuje.
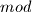
 .
.Potezi su
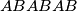 . Primijetimo da ako je zadnja znamenka iz
. Primijetimo da ako je zadnja znamenka iz 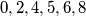 igrač
igrač  gubi. Ako je ta znamenka iz
gubi. Ako je ta znamenka iz 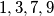 gubitak nije nužan. Zato
gubitak nije nužan. Zato  upisuje jednu od tih znamenaka na kraju, a nijednu prije, jer
upisuje jednu od tih znamenaka na kraju, a nijednu prije, jer  ih treba nastojati ograničiti. Ako su sve znamenke
ih treba nastojati ograničiti. Ako su sve znamenke 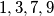 izgubljene na kraju
izgubljene na kraju  nužno gubi.
nužno gubi.Zato sada trebamo gledati djeljivost sa
 .
. 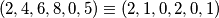 i
i 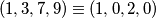 . Imamo nulu viška i to među
. Imamo nulu viška i to među 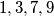 .
.Strategija igrača
 je onda riješiti se brojeva
je onda riješiti se brojeva 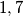 za igrača
za igrača  tako da on na kraju mora napisati
tako da on na kraju mora napisati 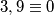 i da da je broj
i da da je broj 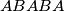 djeljiv s
djeljiv s  .
.To ostvaruje ovako: U prvom i trećem potezu upisuje
 i
i  (poredak je nebitan). Zatim u petom potezu upisuje neku znamenku tako da je broj
(poredak je nebitan). Zatim u petom potezu upisuje neku znamenku tako da je broj 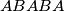 djeljiv s 3.
djeljiv s 3. Zadnja nada igrača
 je ograničiti ostatke igraču
je ograničiti ostatke igraču  . To mu ne uspjeva. Ostatak ako zanemarimo poteze igrača
. To mu ne uspjeva. Ostatak ako zanemarimo poteze igrača  je
je  . S dvama dvojkama ostatak je
. S dvama dvojkama ostatak je  pa
pa  samo igra jednu od
samo igra jednu od  . S dvama jedinicima je
. S dvama jedinicima je  i
i  igra dvojku. S dvama nulama
igra dvojku. S dvama nulama  igra jedinicu. Ako
igra jedinicu. Ako  ne igra na taj način
ne igra na taj način  jednostavno ima sve ostatke na raspolaganju. Dakle,
jednostavno ima sve ostatke na raspolaganju. Dakle,  pobjeđuje.
pobjeđuje. Ocjene: (1)
Komentari:
grga, 4. veljače 2016. 22:31
mislim da bi trebao argumentirati sto ako  izabere u svom prvom potezu
izabere u svom prvom potezu  ili
ili  (onu koju ne odabere
(onu koju ne odabere  ). istina da nije neki pametan slucaj, ali to se moze dogoditi a nisi to pokrio u ovome sto si napisao. inace je tocno, ali je dosta zbrkano zapisano. ako kanis ostvariti neke bodove na natjecanju iskreno ti preporucam da pogledas npr ovdje http://vinkovic.org/Projects/MindExercises/matematika/2009-SS-A.pdf sluzbeno rjesenje.
). istina da nije neki pametan slucaj, ali to se moze dogoditi a nisi to pokrio u ovome sto si napisao. inace je tocno, ali je dosta zbrkano zapisano. ako kanis ostvariti neke bodove na natjecanju iskreno ti preporucam da pogledas npr ovdje http://vinkovic.org/Projects/MindExercises/matematika/2009-SS-A.pdf sluzbeno rjesenje.
 izabere u svom prvom potezu
izabere u svom prvom potezu  ili
ili  (onu koju ne odabere
(onu koju ne odabere  ). istina da nije neki pametan slucaj, ali to se moze dogoditi a nisi to pokrio u ovome sto si napisao. inace je tocno, ali je dosta zbrkano zapisano. ako kanis ostvariti neke bodove na natjecanju iskreno ti preporucam da pogledas npr ovdje http://vinkovic.org/Projects/MindExercises/matematika/2009-SS-A.pdf sluzbeno rjesenje.
). istina da nije neki pametan slucaj, ali to se moze dogoditi a nisi to pokrio u ovome sto si napisao. inace je tocno, ali je dosta zbrkano zapisano. ako kanis ostvariti neke bodove na natjecanju iskreno ti preporucam da pogledas npr ovdje http://vinkovic.org/Projects/MindExercises/matematika/2009-SS-A.pdf sluzbeno rjesenje.  Školjka
Školjka