Točno
6. ožujka 2016. 16:26 (9 godine, 11 mjeseci)
Na ploči su zapisani neki cijeli brojevi. U svakom koraku odabiremo brojeve

i

koji se nalaze na ploči, obrišemo ih i umjesto njih zapišemo brojeve
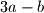
i
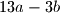
.
Ako su na početku na ploči brojevi
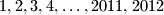
, mogu li se nakon konačnog broja koraka na ploči nalaziti brojevi
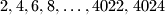
?
%V0
Na ploči su zapisani neki cijeli brojevi. U svakom koraku odabiremo brojeve $a$ i $b$ koji se nalaze na ploči, obrišemo ih i umjesto njih zapišemo brojeve $3a-b$ i $ 13a-3b$.
Ako su na početku na ploči brojevi $1, 2, 3, 4,\ldots, 2011, 2012$, mogu li se nakon konačnog broja koraka na ploči nalaziti brojevi $2,4,6,8,\ldots,4022,4024$?
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Promjena sume svih članova pri transformaciji je:
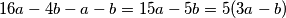
. Dakle ostatak pri dijeljenju sume svih članova s

se neće promijeniti. Ovdje dolazimo do kontradikcije (vidi dole) pa zadatak nije moguće napraviti.
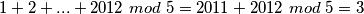
dok je
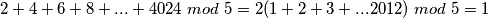
.
%V0
Promjena sume svih članova pri transformaciji je: $16a-4b-a-b=15a-5b=5(3a-b)$. Dakle ostatak pri dijeljenju sume svih članova s $5$ se neće promijeniti. Ovdje dolazimo do kontradikcije (vidi dole) pa zadatak nije moguće napraviti.
$1+2+...+2012 \ mod \ 5 = 2011+2012 \ mod \ 5 = 3$ dok je $2+4+6+8+...+4024 \ mod \ 5 = 2(1+2+3+...2012) \ mod \ 5 = 1$.
| 20. ožujka 2016. 15:09 | ikicic | Točno |