Točno
12. listopada 2017. 16:20 (7 godine, 2 mjeseci)
Neka je
prirodan broj koji se može prikazivati kao suma kvadrata dvaju prirodnih brojeva na dva različita načina:
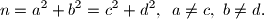
Dokažite da je
složen broj.
%V0
Neka je $n$ prirodan broj koji se može prikazivati kao suma kvadrata dvaju prirodnih brojeva na dva različita načina:
$$n=a^2+b^2=c^2+d^2, \,\,\, a \neq c, \,\, b \neq d.$$
Dokažite da je $n$ složen broj.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Imamo da $\{|a|, |b|\} \cap \{|c|, |d|\} = \emptyset$.
Pretpostavimo suprotno, da je $n$ prost.
$$n = (a+bi)(a-bi) = (c+di)(c-di)$$
Zbog svojstava $\mathbb{Z}[i]$ imamo da su $a+bi, a-bi, c+di, c-di$ prosti u $\mathbb{Z}[i]$. (prosti su svi $z$ takvi da je $\text{N}(z)$ prosto u $\mathbb{N}$)
Međutim, faktorizacija u $\mathbb{Z}[i]$ je jedinstvena do na množenje sa četvrtim korijenom iz jedinice, pa mora biti $\{|a|, |b|\} = \{|c|, |d|\}$, što je u kontradikciji sa pretpostavkom zadatka.
| 30. studenoga 2018. 23:57 | iivan | Točno |
Školjka 
.
Zbog svojstava ![\mathbb{Z}[i]](/media/m/c/3/e/c3eadb8cecf982877b60354ff97aaec7.png)
imamo da su 
prosti u 
takvi da je 
prosto u 
)
, što je u kontradikciji sa pretpostavkom zadatka.