Kliknite ovdje kako biste prikazali rješenje.
Primjenimo adicijsku formulu na LHS zadanog izraza
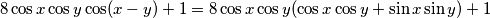
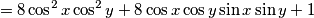
Oduzmemo RHS s obije strane i pojednostavimo izraz koristeći Pitagorin poučak 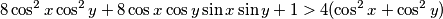
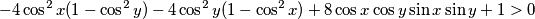
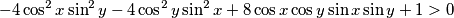
Daljnjim grupiranjem i primjenom adicijskih formula nejednakost se svodi na
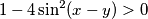
odnosno
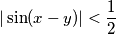
Ako je 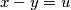 , ova nejednakost će vrijedi za
, ova nejednakost će vrijedi za 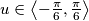 i početna tvrdnja će biti dokazana.
i početna tvrdnja će biti dokazana.
S obzirom da imamo izbor 4 broja iz intervala 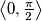 po Dirichletovom principu barem 2 od ta broja biti će u intervalu
po Dirichletovom principu barem 2 od ta broja biti će u intervalu 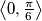 ili u intervalu
ili u intervalu 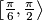 .
.
Ako su zadana dva broja u intervalu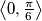 , njih izabremo kao x i y i nejednakost će vrijediti.
, njih izabremo kao x i y i nejednakost će vrijediti.
Ako nisu zadana dva broja u intervalu 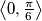 onda mora biti zadano barem tri broja u intervalu
onda mora biti zadano barem tri broja u intervalu 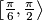 . Kada bi mogli izabrati dva broja tako da nejednakost ne vrijedi, razlika između ta dva broja bi morala biti veća od
. Kada bi mogli izabrati dva broja tako da nejednakost ne vrijedi, razlika između ta dva broja bi morala biti veća od 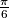 . No s obzirom da postoje tri broja u intervalu
. No s obzirom da postoje tri broja u intervalu 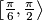 , to nije moguće (
, to nije moguće (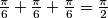 ) i uvijek ćemo moći izabrati dva broja čija je razlika manja od
) i uvijek ćemo moći izabrati dva broja čija je razlika manja od 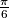 . Time je nejednakost dokazana.
. Time je nejednakost dokazana.
 Školjka
Školjka 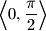 moguće odabrati dva broja, nazovimo ih
moguće odabrati dva broja, nazovimo ih  i
i  , tako da vrijedi
, tako da vrijedi