U svako polje kvadratne ploče 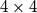 upiši po jedno od četiri slova:
upiši po jedno od četiri slova:  ,
,  ,
,  ,
,  , i po jedan od četiri broja:
, i po jedan od četiri broja:  ,
,  ,
,  ,
,  , tako da budu ispunjeni sljedeći uvjeti:
, tako da budu ispunjeni sljedeći uvjeti:
 u svakom retku i u svakom stupcu svako od tih slova i svaki od tih brojeva pojavljuje se točno jednom;
u svakom retku i u svakom stupcu svako od tih slova i svaki od tih brojeva pojavljuje se točno jednom;
 na ploči se svaka kombinacija (par) jednog slova i jednog broja nalazi na točno jednom polju.
na ploči se svaka kombinacija (par) jednog slova i jednog broja nalazi na točno jednom polju.
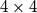 upiši po jedno od četiri slova:
upiši po jedno od četiri slova:  ,
,  ,
,  ,
,  , i po jedan od četiri broja:
, i po jedan od četiri broja:  ,
,  ,
,  ,
,  , tako da budu ispunjeni sljedeći uvjeti:
, tako da budu ispunjeni sljedeći uvjeti: u svakom retku i u svakom stupcu svako od tih slova i svaki od tih brojeva pojavljuje se točno jednom;
u svakom retku i u svakom stupcu svako od tih slova i svaki od tih brojeva pojavljuje se točno jednom; na ploči se svaka kombinacija (par) jednog slova i jednog broja nalazi na točno jednom polju.
na ploči se svaka kombinacija (par) jednog slova i jednog broja nalazi na točno jednom polju. Slični zadaci
Ivan, Stipe i Tonći izmjenjuju se u bacanju kockice. Prvi baca Ivan, onda Stipe pa Tonći, i nakon toga opet Ivan i tako dalje istim redom. Svaki od njih, kad je njegov red, baca kockicu jednom, sve dok ne dobije prvu šesticu. Nakon što dobije svoju prvu šesticu, u svakom idućem bacanju Ivan baca kockicu četiri, Stipe šest, a Tonći osam puta.
Tonći je zadnji dobio prvu šesticu, u svom desetom bacanju, i tada je igra završila. Ako je kockica bačena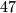 puta, odredi tko je od njih kockicu bacao najviše puta.
puta, odredi tko je od njih kockicu bacao najviše puta.
Tonći je zadnji dobio prvu šesticu, u svom desetom bacanju, i tada je igra završila. Ako je kockica bačena
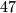 puta, odredi tko je od njih kockicu bacao najviše puta.
puta, odredi tko je od njih kockicu bacao najviše puta.  Školjka
Školjka  prirodan broj. Dokaži da je broj neparnih brojeva među brojevima
prirodan broj. Dokaži da je broj neparnih brojeva među brojevima 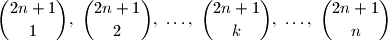 neparan.
neparan. 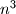 (
(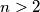 ) jednakih kockica. Ako je poznato da je broj kockica, kojima je točno jedna strana obojana, jednak broju kockica kojima niti jedna strana nije obojana, odredi broj
) jednakih kockica. Ako je poznato da je broj kockica, kojima je točno jedna strana obojana, jednak broju kockica kojima niti jedna strana nije obojana, odredi broj  ,
,  ,
,  ,
, 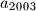 cijeli brojevi i
cijeli brojevi i 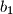 ,
, 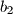 ,
, 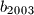 ti isti brojevi poredani na neki drugi način, dokažite da je produkt
ti isti brojevi poredani na neki drugi način, dokažite da je produkt 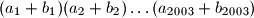 paran broj.
paran broj. 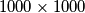 obojano je crnom ili bijelom bojom. Ukupan broj crnih polja na ploči je za
obojano je crnom ili bijelom bojom. Ukupan broj crnih polja na ploči je za 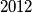 veći od ukupnog broja bijelih polja. Dokaži da postoji kvadrat
veći od ukupnog broja bijelih polja. Dokaži da postoji kvadrat 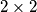 koji sadrži tri polja jedne boje i jedno polje druge boje.
koji sadrži tri polja jedne boje i jedno polje druge boje.