Na željezničkoj pruzi dugačkoj
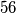
km ima

postaja

,
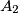
, ...,
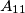
. Udaljenosti oblika
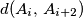
, (
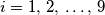
) nisu veće od

km, a udaljenosti oblika
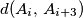
, (
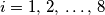
) nisu manje od

km. Kolika je udaljenost
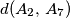
?
%V0
Na željezničkoj pruzi dugačkoj $56$ km ima $11$ postaja $A_1$, $A_2$, ..., $A_{11}$. Udaljenosti oblika $d\!\left(A_i,\,A_{i+2}\right)$, ($i=1,\,2,\,\ldots,\,9$) nisu veće od $12$ km, a udaljenosti oblika $d\!\left(A_i,\,A_{i+3}\right)$, ($i=1,\,2,\,\ldots,\,8$) nisu manje od $17$ km. Kolika je udaljenost $d\!\left(A_2,\,A_7\right)$?