Odredite jednadžbu pravca

koji prolazi točkom
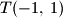
, a polovište segmenta kojeg na

odsjecaju pravci
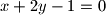
i
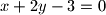
leži na pravcu
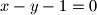
.
%V0
Odredite jednadžbu pravca $p$ koji prolazi točkom $T(-1,\,1)$, a polovište segmenta kojeg na $p$ odsjecaju pravci $x + 2y - 1 = 0$ i $x + 2y - 3 = 0$ leži na pravcu $x - y - 1 = 0$.