Neka je
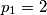
,
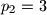
,
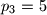
,

,
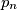
,

niz svih prostih brojeva poredanih po veličini. Dokažite da za svaki prirodan broj

vrijedi nejednakost
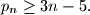
%V0
Neka je $p_1 = 2$, $p_2 = 3$, $p_3 = 5$, $\dots$, $p_n$,$\dots$ niz svih prostih brojeva poredanih po veličini. Dokažite da za svaki prirodan broj $n$ vrijedi nejednakost $$
p_n \ge 3n - 5.
$$