Školjka

%V0 U pravokutnom trokutu težišnica i simetrala pravog kuta dijele hipotenuzu na tri dijela čije duljine, u nekom poretku, čine aritmetički niz. Odredi sve moguće omjere duljina kateta tog trokuta. [i]Tri broja čine aritmetički niz ako je suma najmanjeg i najvećeg jednaka dvostrukom srednjem broju.[/i]

%V0 Ako su duljine stranica trokuta tri uzastopna člana aritmetičkog niza, dokaži da su tada kotangensi polovičnih kutova tog trokuta također uzastopni članovi nekog aritmetičkog niza.

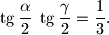
%V0 Ako su u trokutu duljine stranica $a$, $b$, $c$ tri uzastopna člana aritmetičkog niza (u tom poretku), dokažite da za njegove kutove ($\alpha $ je kut nasuprot stranice $a$, $\gamma $ nasuprot stranice $c$) vrijedi: $$ \tg \dfrac{\alpha}{2}\;\tg \dfrac{\gamma}{2}=\dfrac{1}{3}. $$

%V0 Na krakovima šiljastog kuta $\alpha $ s vrhom $A$ dane su točke $D$ i $E$, tako da je $|AD|=m$ i $|AE|=n$. U točkama $D$ i $E$ povučene su okomice na krakove kuta na kojima leže. Ako se te dvije okomice sijeku u točki $F$ u unutrašnjosti kuta, dokažite da je $$ \frac{|DF|}{|EF|}=\frac{n-m\cos \alpha }{m-n\cos \alpha }. $$

%V0 U elipsu $ b^2x^2+a^2y^2=a^2b^2 $ (sa središtem u ishodištu), upisan je trokut $ ABC $ tako da je tangenta na elipsu u svakom njegovom vrhu paralelna s nasuprotnom stranicom trokuta. Kolika je površina tog trokuta ako je $C=(0,b)$?

%V0 Za koje trokute vrijedi jednakost $$ \tg (\alpha -\beta )+\tg (\beta -\gamma )+\tg (\gamma -\alpha )=0, $$ ako su $\alpha $, $\beta $ i $\gamma $, kutovi trokuta?