U elipsu
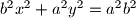
(sa središtem u ishodištu), upisan je trokut

tako da je tangenta na elipsu u svakom njegovom vrhu paralelna s nasuprotnom stranicom trokuta. Kolika je površina tog trokuta ako je
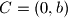
?
%V0
U elipsu $ b^2x^2+a^2y^2=a^2b^2 $ (sa središtem u ishodištu), upisan je trokut $ ABC $ tako da je tangenta na elipsu u svakom njegovom vrhu paralelna s nasuprotnom stranicom trokuta. Kolika je površina tog trokuta ako je $C=(0,b)$?