neka je

tocka na simetrali kuta

trokuta

, a

i

redom tocke na stranicama

i

, takve da je
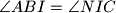
i
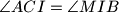
. dokazite da je

srediste upisane kruznice trokuta

ako i samo ako su tocke

,

i

kolinearne.
%V0
neka je $I$ tocka na simetrali kuta $\angle BAC$ trokuta $ABC$, a $M$ i $N$ redom tocke na stranicama $\overline{AB}$ i $\overline{AC}$, takve da je $\angle ABI = \angle NIC$ i $\angle ACI = \angle MIB$. dokazite da je $I$ srediste upisane kruznice trokuta $ABC$ ako i samo ako su tocke $M$, $N$ i $I$ kolinearne.